|
Задача поиска документов по образцу предпологает решение
двух основных задач:
- тематическая классификация текстовой информации;
- вычисление степени тематической принадлежности текста к
заданному классу.
Эти задачи связаны, прежде всего, с анализом текста, а
именно, с анализом смыслового содержания текста, его тематической
направленности.
Всю совокупность представленных на сегодняшний день методов
анализа текста, относительно задачи анализа его содержания, можно разделить на
две большие группы:
- лингвистический анализ;
- статистический анализ.
Первый ориентирован на извлечении смысла текста по его
семантической структуре. Второй – по частотному распределению слов в тексте.
В данной работе было принято решение использовать методы статистического
анализа в силу их относительной простоты, удобства использования и языковой
независимости. Методы лингвистического анализа, хотя и позволяют точнее
анализировать текст, выделяя его структурные особенности, но являются более
трудоемкими и сложными в использовании. Связано это, прежде всего, с богатством
семантики и морфологии естественных языков. Формальное описание правил
естественного языка и их реализация – весьма трудоемкий процесс, требующий
привлечения специалистов из области лингвистики. Кроме того, лингвистический
анализ предполагает ориентацию на конкретный язык с его конкретными
семантическими особенностями, это обуславливает его плохую межъязыковую
переносимость. Работы в данном направлении идут [10, 24, 123], и существует
множество практических реализаций, но на сегодняшний день лингвистический
анализ по части анализа семантики весьма проблематичен.
Все это обусловило целесообразность применения
статистических методов для решения задач данной работы. Однако частотный анализ,
используемый в настоящее время при определении тематики документов [120], не
позволяет в полной мере учесть внутреннюю структуру текста, т.к. при таком анализе
не учитывается связность и последовательность текста. Хотя именно связность текста
(речевого высказывания) считается одним из важнейших условий, необходимых для понимания
его смыла и содержания. Данное положение является ключевым как в
психолингвистике [3, 27], так и нейропсихологии [1, 18].
В ряде работ [11, 28] в области информационного поиска также
отмечается эта особенность. Опираясь на результаты этих исследований, а также результаты
собственных исследований [29, 30, 32], автором была разработана модель структурного
представления текста, учитывающая его связность [34, 35].
Суть предлагаемого подхода заключается в моделировании
структуры текста информационным потоком и формировании этим потоком ориентированного
мультиграфа, вершинами которого являются слова, а ребрами – связи между словами
в тексте. Этот мультиграф является информационной структурой текста [34, 35].
Мультиграф – это граф, который может содержать множество
ребер соединяющих одну и туже пару вершин.
Информационный поток – это детерминированный поток событий,
принадлежащих некоторому конечному множеству. Временной интервал между
событиями нас не интересует, интересует только последовательность событий. В
данном случае события – это слова, а конечное множество – это множество всех
слов, присутствующих в анализируемом тексте. Информационный поток эквивалентен
временному ряду номинальных (категориальных) величин.
Под информационной структурой понимается совокупность всех событий
и связей между ними. Для информационной структуры текста связи между событиями
– это словосочетания.
Информационный поток, по сути, моделирует динамику
некоторого процесса, в данном случае текста, а информационная структура является
статическим представлением информационного потока.
Переход к модели структурного представления текста осуществляется
следующим образом.
1) Текст рассматривается в виде информационного потока,
образованного информационными элементами - словами.
Если последовательно брать слова из текста, начиная с самого
первого и кончая последним, то это как раз и будет информационный поток F.
При этом набор всех слов в тексте можно выделить в конечное
множество уникальных информационных элементов:
I = {i1, i2, ..., in},
где i – информационный элемент соответствующий определенному слову из текста.
Информационный поток F будет представлен в виде последовательного чередования этих
элементов (рис. 2.1).
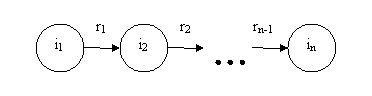
Рис. 2.1. Информационный поток
F = (i1, i2, ..., in).
Информационный поток также может быть представлен в виде
набора связей:
F = (r1, r2, ..., rn-1),
где: ri = (ii, ii+1)
– связь между двумя информационными элементами, последовательно идущими в
информационном потоке.
Далее, чтобы не перегружать рисунки избыточной информацией, будем
опускать именование связей.
Порядок чередования информационных элементов зависит от их
последовательности в тексте. Информационные элементы в потоке могут повторяться.
Обязательное условие – однозначное соответствие информационного элемента слову
из текста. Одинаковые слова в тексте соответствуют одному и тому же
информационному элементу.
Пример.
Фрагмент текста: “Дао, которое может быть выражено словами
не есть постоянное Дао. Имя, которое может быть названо, не есть постоянное имя”.
Из данного набора слов выделяем множество уникальных
информационных элементов (различия в регистре и знаки препинания не учитываются):
I = {i1, i2, i3, i4, i5,
i6, i7, i8, i9, i10, i11},
где:
i1 = быть,
i2 = выражено,
i3 = дао,
i4 = есть,
i5 = имя,
i6 = которое,
i7 = может,
i8 = названо,
i9 = не,
i10 = постоянное,
i11 = словами.
Информационный поток соответствующий данному фрагменту
текста (рис. 2.2) будет представлен в виде набора информационных элементов:
F = (i3, i6, i7, i1,
i2, i11, i9, i4, i10, i3,
i5, i6, i7, i1, i8, i9,
i4, i10, i5)

Рис. 2.2. Информационный поток, соответствующий заданному тексту
2) Поток формирует структуру.
Если учесть, что слова в тексте повторяются, то,
соответственно, можно допустить, что информационный поток будет многократно
проходить через одни и те же информационные элементы, формируя, таким образом,
связанную информационную структуру текста.
Для вышеприведенного фрагмента текста данная структура будет
выглядеть следующим образом (рис. 2.3).

Рис. 2.3. Структура, формируемая информационным потоком
Тезис о том, что информационный поток будет многократно
проходить через одни и те же информационные элементы, носит принципиальный характер,
при отсутствии циклов графа, образованных информационным потоком, ни о какой
формируемой структуре не приходится говорить.
На самом деле структура, представленная на рис.2.3, не
отражает в полной мере информационный поток, описывающий фрагмент текста.
Необходимо дополнить эту структуру информацией о прохождении потока через
каждый из информационных элементов. Для каждого повторного прохождения потока
через одну и ту же пару информационных элементов необходимо формировать
дополнительные связи – ребра. Тогда структура описывается в виде мультиграфа –
графа, который может содержать множество ребер соединяющих одну и ту же пару
вершин.
Для удобства отображения такого мультиграфа проиндексируем
информационный поток и припишем каждому ребру графа, соединяющего пару вершин,
множество индексов, соответствующих прохождению информационного потока через
данную пару.
Рассмотрим в качестве примера все тот же фрагмент текста,
который описывается информационным потоком:
F = (i3, i6, i7, i1,
i2, i11, i9, i4, i10, i3,
i5, i6, i7, i1, i8, i9,
i4, i10, i5).
Индексация данного информационного потока будет означать,
что каждому переходу между двумя информационными элементами будет поставлен в
соответствие индекс, начиная с единицы, с последовательным его инкрементом.
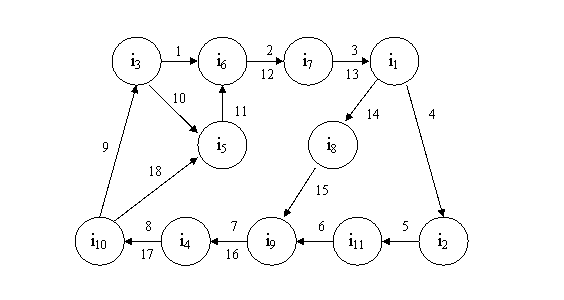
Рис. 2.4. Индексированная структура информационного потока
Информационная структура, приведенная на рис. 2.4, в полной
мере отражает все особенности потока, описывающего фрагмент текста.
Весьма показательным является приведенный выше фрагмент
текста, особенность его, прежде всего, в том, что для сравнительно небольшого количества
слов, входящих в данный фрагмент, существуют циклы. И информационный поток,
моделирующий данный фрагмент, формирует явно выраженную структуру. Лингвистический
анализ текста, его стилистические особенности и смысловая многозначность
выходят за рамки диссертационной работы, но некоторая корреляция, по-видимому,
существует между информативностью и структурной насыщенностью - наличием
большого числа связей между отдельными элементами. Явно выражен принцип
усложнения системы за счет введения дополнительных связей между отдельными
элементами.
Введем дополнительные обозначения и определим некоторые важные
характеристики информационной структуры.
n(I) = | I | - количество информационных элементов множества I (количество уникальных слов в тексте).
n(F) = | F | - количество информационных элементов набора F (общее количество слов в тексте).
M(I, R) – информационная структура
(ориентированный мультиграф). Является совокупностью I - множества информационных
элементов (вершин графа) и R - набора связей между этими элементами (ребер
графа).
M(I, R)  F. F.
R - набор связей между парами информационных элементов,
может содержать повторяющиеся связи в случае многократного прохождения информационного
потока F через одни и те же пары элементов.
R = (r1, r2, ..., rn-1),
где: r = (ii, ii+1)
– связь между двумя информационными элементами, обозначает последовательность
информационных элементов ii, ii+1 в потоке F.
 . .
Для каждого информационного элемента из множества I, входящего в структуру M(I, R), существует набор пар связей,
где: ri, rj
– входная связь, ri+1, rj+1 – выходная связь, n – число пар
связей.
Входная означает, что данная связь предшествует выходной в
наборе связей, описывающих поток, проходящий через данный информационный
элемент. Если проиндексировать связи в наборе, описывающие поток, то индекс
входной связи будет на единицу меньше выходной.
n(R(i)) - количество пар связей в наборе R(i).
Характеризует число связей данного информационного элемента с
другими информационными элементами в структуре M(I, R). n(R(i)) равно числу повторений слова в
тексте.
Обозначим количество пар связей как:
d(i) – степень
информационного элемента
d(i) = n(R(i)),
 , ,
 . .
d(M(I, R))max
– максимальная степень информационного элемента для информационной структуры M(I, R):
d(M(I, R))max = max d(i), 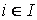 . .
d(M(I, R))min
– минимальная степень информационного элемента для информационной структуры M(I, R):
d(M(I, R))min = min d(i), 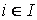 . .
r+(F,
ik, ij, e), r-(F,
ik, ij, e) – расстояние между двумя информационными элементами в
потоке F, 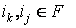 , ,
где:
e – вхождение информационного элемента ik в поток F, его порядковый номер в потоке.
r+ - означает, что расстояние измеряется по ходу информационного потока.
r- - означает, что расстояние измеряется обратно ходу информационного потока.
Расстояние измеряется в количестве информационных элементов находящихся между ik и ij, плюс 1.
Пример:
F = (i2, i5, i1, i4, i5, i2, i3)
r+(F, i2, i3, 1) = 6
r+(F, i2, i3, 2) = 1
r-(F, i1, i2, 1) = 2
r-(F, i1, i3, 1) = 0
r+(F, i1, i3, 1) = 4
0 – означает, что результат не определен
rmin(F, ik, ij) –
минимальное расстояние между двумя информационными элементами в потоке, 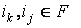 . .
Пример:
F = (i2, i6, i1, i4, i5, i7, i2)
rmin(F, i2, i5) = 2
rmin(F, i1, i2) = 2
rmin(F, i1, i8) = 0
Информационный поток относительно некоторого информационного
элемента i можно описать как:
F(i, e, [r-, r+]),
где e –
вхождение информационного элемента ik в поток F, его порядковый номер в
потоке; [r-, r+]
– окрестность, для которой определяется поток.
F(i, e, [r-, r+]) = (i - r-,
..., i - 2, i - 1, i, i + 1, i + 2, ..., i + r+),
где
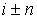 - обозначает
индексацию некоторого информационного элемента в наборе F относительно информационного элемента i;
i + 1 – обозначает информационный элемент, следующий сразу за i в информационном потоке F;
i - 1 – обозначает информационный элемент, предшествующий i, в информационном потоке F. - обозначает
индексацию некоторого информационного элемента в наборе F относительно информационного элемента i;
i + 1 – обозначает информационный элемент, следующий сразу за i в информационном потоке F;
i - 1 – обозначает информационный элемент, предшествующий i, в информационном потоке F.
Пример:
F = (i2, i5, i1, i4, i5, i2, i3, i8, i10, i1)
F(i4, 1, [3, 3]) = (i2, i5, i1, i4, i5, i2, i3)
F(i2, 2, [2, 4]) = (i4, i5, i2, i3, i8, i10, i1)
F(i2, 1, [2, 2]) = (0, 0, i2, i5, i1)
F(i5, 1, [2, 5]) = (0, i2, i5, i1, i4, 0, 0, 0)
Необходимо сделать одно уточнение - не всегда будет
существовать поток для всей окрестности.
Такая ситуация возможна, когда заданный информационный
элемент находится близко к началу или концу информационного потока,
описывающего текст, т.е. элементов i - r-, ..., i - 2, i - 1 и i + 1, i
+ 2, ..., i + r+
может просто не существовать, или существовать только часть их, в
зависимости от того, насколько близок элемент i к началу или концу текста.
Также такая ситуация возможна в том случае, когда циклы,
формируемые потоком, многократно проходящим через i, имеют
меньше информационных элементов, чем выбранное r.
В таких случаях будем принимать равным 0, все элементы,
которые не определены в данной окрестности.
Обозначим множество всех информационных потоков относительно
информационного элемента i для всех его вхождений в
поток F:
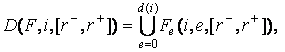
Пример:
F = (i2, i5, i1, i4, i5, i2, i3, i8, i5, i1),
d(i5) = 3,
D(F, i5, [2, 2]) = ((0, i2, i5, i1, i4), (i1, i4, i5, i2, i3), (i3, i8, i5, i1, 0)).
На базе представленной модели выполним разработку метода и
алгоритмов тематического анализа текста для решения двух основных задач данной
работы:
- тематической классификации текстовой информации;
- вычисления степени тематической принадлежности текста к
заданному классу.
Предлагаемый подход к тематической классификации текстовой
информации основывается на гипотезе о том, что словарный запас и частоты использования
слов зависят от темы текста [21, 120]. В настоящее время данная гипотеза
активно и успешно используется в тематико-ориентированных методах поиска [72, 120,
48, 114, 115].
Тематическая классификация предполагает выделение множества
ключевых слов, определяющих тематику текста. При этом каждому из них приписывается
вес, определяющий значимость данного слова в тематике, т.е. какие-то ключевые
слова играют большую роль в определении тематики, какие-то меньшую, но именно
такая совокупность слов, с такой значимостью каждого из них в тематике и определяет
тематическую направленность.
Такой подход обеспечивает снижение размерности решаемой
задачи за счет перехода от основного текста к его представлению в виде
множества ключевых слов, приближенно описывающих его содержание. Это
необходимо, прежде всего, для последующей тематической идентификации сравниваемых
текстов. Задача классификации в данном случае сводится к задаче отнесения текста
к некоторому тематическому классу, описываемому множеством ключевых слов.
Замечание: тематические классы в этом случае не определены
заранее, их формирование, а также идентификация и отнесение текста к тому или
иному классу происходит в процессе анализа текста.
Ключевые слова определяются по количеству их вхождений в
текст, а именно – частота ключевых слов в тексте выше других слов. В рамках
рассматриваемой модели структурного представления текста это будет означать,
что через данные слова чаще проходит информационный поток, и информационные
элементы, соответствующие этим словам, имеют большее количество связей с
другими информационными элементами.
Проблема заключается в определении порога (автоматизированном,
машинном определении), который отделяет ключевые слова от всех остальных.
Очевидно, выбор пороговой величины должен зависеть от конкретного
текста, от таких характеристик модели как d(M(I, R))max, d(M(I, R))min
и n(I).
Однако этого не достаточно, чтобы корректно выделять
тематику текста. Адекватность тематики (машинного представления темы текста, в
виде множества ключевых слов) по отношению к теме, которую для себя определяет
человек после чтения текста, вопрос открытый.
Автором выдвигается гипотеза о том, что корректное и
адекватное машинное представление тематики текста должно включать в себя не
только ключевые слова, но и контекст этих слов, т.к. смысл любого слова
определяется исключительно в контексте тех слов, которые употреблялись вместе с
ним, близко, рядом по тексту. И сами по себе ключевые слова в отрыве от их
контекста не отражают в полной мере тематическую направленность текста. Существующие
исследования в психолингвистике [2, 3, 27] подтверждают данный тезис.
Необходимость дополнения ключевых слов контекстом
определяется также соображениями практического характера. Суть этих соображений
заключается в следующем.
Особенности частотного распределение слов в тексте могут
значительно затруднить выбор пороговой величины и снизить качество последующего
анализа документов на тематическую близость. Например, ситуация частотного
выброса одного из слов. Непонятно при этом, какой необходимо устанавливать
порог отсева, если частота повторений одного слова значительно превосходит все
остальные, а все остальные при этом имеют одинаковую частоту. Либо
устанавливать порог для выделения одного ключевого слова, или опускать порог и
брать все слова текста в качестве тематики. И тот, и другой вариант
неприемлемы, в одном случае тематика текста будет представлена в виде одного
слова, в другом - тематикой будут все слова. Организация последующего поиска
тематически близких документов (текстов), на основе множества ключевых слов,
выступающих в качестве поискового запроса, представляется в этом случае весьма
проблематичной. Если поисковый запрос представлен одним словом – результат поиска
может дать незначительное число тематически близких документов, если поисковый
запрос представлен всеми словами документа, то результат поиска может дать слишком
много “тематически далеких” документов (рассматривается вариант поиска – искать
документы, содержащие хотя бы одно из слов запроса).
Дополнение ключевых слов контекстом в этом случае является
вполне разумным и приемлемым вариантом решения данной проблемы.
Приступим к разработке метода тематической классификации на
основе модели структурного представления текста, учитывая вышеприведенные
соображения.
Общая последовательность метода будет выглядеть следующим
образом.
- Моделирование текста и формирование информационной структуры M(I, R).
- Выделение множества всех информационных элементов, ранжированных по их степени d(i)
(числу повторений в тексте). Элемент с d(M(I, R))max будет первым, и далее по убыванию.
- Выделение множества ключевых элементов. Из множества всех информационных элементов (полученных на
предыдущем этапе) берем n первых (n определяется на основе пороговой величины), которые будут
первичным множеством ключевых элементов Sp = {k1i1,
k2i2, ..., knin}. Коэффициенты k1,
k2, ..., kn – соответствуют степеням информационных элементов.
- Формирование уточняющего множества Ss, на основе контекстного анализа информационных
элементов множества Sp.
- Получение общего множество ключевых элементов, определяющее тематику текста: S = Sp
+ Ss.
Суть метода заключается в том, чтобы выделить первичный
набор ключевых элементов за счет количества их повторений в тексте и затем
дополнить его контекстом, на основе анализа структурных особенностей
мультиграфа.
Первые три пункта вряд ли нуждаются в дополнительных
комментариях, рассмотрим подробнее порядок формирования множества Ss.
Одним из ключевых моментов является тот факт, что через
информационный элемент поток может проходить множество раз. Тем более это
справедливо для первичного множества ключевых элементов Sp,
т.к. именно они выбраны из всего текста на том основании, что у них больше
связей с другими информационными элементами. Окрестность информационного
элемента, а это множество информационных элементов, входящих в D(F, i, [r-, r+]),
в этом случае является контекстом. Анализ окрестности информационного элемента для
выделения контекста данного элемента будем называть контекстным анализом.
Формирование множества Ss,
на основе контекстного анализа информационных элементов множества Sp выглядит следующим образом.
1) Выделяем в набор A(i) множество всех потоков проходящих через каждый информационный
элемент  , в
некоторой окрестности заданной r. , в
некоторой окрестности заданной r.
A(i) = D(F, i, [r-, r+]),
r- = r; r+ = r.
A(i) = D(F, i, [r, r]) .
Объединяем все наборы A(i), для каждого  в один общий набор A(Sp): в один общий набор A(Sp):

Обозначим его A:
A = A(Sp).
В результате мы получили общий набор A,
включающий в себя все потоки, проходящие через информационные элементы
множества Sp, в некоторой окрестности
заданной r.
2) Исключаем все информационные элементы из A, принадлежащие Sp:
A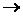 A’, A’,
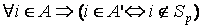 . .
3) Теперь из набора информационных элементов A’ выделяем множество
информационных элементов Ss:
A’ Ss. Ss.
При этом будем учитывать количество повторяющихся информационных элементов и для каждого элемента
множества Ss запишем число их повторений в наборе A’: Ss = {k1i1,
k2i2, ..., knin}, коэффициенты k1, k2,
..., kn перед i – это число повторений этих информационных элементов в наборе A’.
Все элементы множества Ss
присутствуют в некоторой окрестности элементов множества Sp,
и каждый информационный элемент 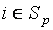 определяет центр некоторой окрестности в
информационной структуре M(I, R). Окрестность задается по информационным потокам,
проходящим через i. определяет центр некоторой окрестности в
информационной структуре M(I, R). Окрестность задается по информационным потокам,
проходящим через i.
На рис. 2.5 приведен пример выделения окрестности информационного
элемента i5 некоторой информационной
структуры (на рисунке приведен ее фрагмент), при r = 1.

Рис. 2.5. Выделение окрестности
Для данного примера Ss = {i45, i3, i22, i10,
i4, i32}, все коэффициенты равны 1.
Если рассматривать текст, то это означает, что для
некоторого слова определяются все его вхождения в текст. Затем для каждого из
вхождений определяются соседние с ним слова в пределах некоторого
диапазона-окрестности r (вперед и назад по тексту). После
этого подсчитываются повторения всех слов, которые встретились в диапазоне
каждого из вхождений. Число повторений затем используется для определения весов
этих слов в тематике.
Нужно отметить одну важную деталь, а именно, окрестности
ключевых элементов из Sp, могут пересекаться,
если ключевые слова расположены в тексте рядом (в пределах r).
Тогда при подсчете повторяющихся информационных элементов необходимо учитывать
их индекс в информационном потоке и не считать повторно информационный элемент
с одним и тем же индексом, чтобы веса элементов из множества Ss не превышали веса элементов множества Sp,
так как мы определяем значимость данных элементов в тематике.
В итоге мы получаем общее множество ключевых элементов
определяющих тематику текста:
S = Sp + Ss,
S = {k1i1, k2i2, ..., knin}.
Весовые коэффициенты k1, k2, ..., kn,
определяют значимость того или иного информационного элемента в данной тематике.
Размер текста. Необходимо отдельно
оговорить размер анализируемых текстовых фрагментов. Существует ограничения на
размер текстового фрагмента, обусловленные использованием метода частотного
анализа.
Главным образом, ограничения касаются не столько размера
текстового фрагмента, сколько соотношения количества уникальных слов (множество
слов, из которых сформирован данный текстовый фрагмент) к общему их количеству:
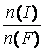 . .
Пользуясь приведенным соотношением, можно оценить
адекватность анализа тематики для конкретного текстового фрагмента. Чем ближе
соотношение к 1, тем менее корректно выделение тематики. Соотношение, равное 1,
означает, что тематикой будут все слова текста.
Ключевые слова, определяющие тему документа, должны
встречаться в тексте чаще других слов, только при выполнении этого условия
правомерно говорить о выделении тематики. Сказать насколько чаще они должны
встречаться, затруднительно в силу многообразия текстов и исключительной
субъективности самого понятия темы текста.
Эмпирический подбор коэффициента, определяющего границу,
порог адекватности, возможен в рамках конкретной поисковой системы с учетом
специфики анализируемых документов. Выбор конкретного порога или реализация
оценки адекватности анализа того или иного текста на основе приведенного
соотношения – это прерогатива разработчика поисковой системы.
Использование описательных статистик и вероятностных
распределений для анализа этой величины затруднено, так они ориентированны на
порядковые переменные. Специфика статистического анализа в нашем случае такова,
что анализируются категориальные (номинальные) величины – слова, относящиеся к
так называемым бедным шкалам измерений [4]. Одним из вариантов анализа в данном
случае может быть анализ таблиц частот распределения этих величин и анализ
экспертных оценок эффективности выделения тематики для тех или иных
соотношений 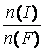 . .
Детальное рассмотрение этого вопроса требует дополнительной
теоретической проработки и экспериментальных исследований, выходящих за рамки
данной работы.
Параметры. Остается отметить, что
данный метод выделения тематики также зависит от двух параметров:
- пороговой величины – определяющей ключевые слова;
- расстояния r – задающего окрестность.
Вариации этих параметров могут в значительной мере влиять на
результат выделения тематики. При этом оценить адекватность и корректность
выбора той или иной комбинации параметров можно только на основе вычисления тематической
близости текстов (по выделенной тематике) и оценки ее экспертом. Более
подробно этот вопрос рассмотрим далее.
Приступим к решению второй задачи данной работы – задаче вычисления
степени тематической принадлежности текста к образцу.
Есть текст-образец, и есть некоторый произвольный текст, необходимо
количественно оценить, насколько близка тематика произвольного текста к тематике
заданного текста образца, т.е. вычислить степень тематической принадлежности
текста к образцу. Далее для краткости будем использовать термин тематическая близость.
И произвольный текст, и текст-образец могут быть
представлены в виде тематических классов, метод частотно-контекстной классификации,
представленный в предыдущем параграфе позволяет это сделать. Теперь необходимо
разработать алгоритм вычисления тематической близости двух произвольных
тематических классов, заданных множествами ключевых элементов (слов).
Пусть:
S – множество ключевых элементов текста образца:
S = {k1i1, k2i2, ..., knin},
где коэффициенты k1, k2, ..., kn перед i –
это веса информационных элементов, определяющие значимость данного элемента в
тематике текста образца.
Sf – множество ключевых
элементов некоторого найденного в результате поиска текста (документа
найденного информационно-поисковой системой), который нам необходимо
проанализировать на тематическую близость по отношению к тексту образцу
Sf = {kf1i1, kf2i2,
..., kfnin},
где коэффициенты kf1, kf2, ..., kfn перед i –
это веса информационных элементов, определяющие значимость данного элемента в тематике найденного текста.
При этом информационные элементы i1, i2, ..., in
определяющие тематику обоих множеств S и Sf соотносятся между собой, т.е.
информационный элемент i1 из множества S, идентичен информационному элементу i1
из множества Sf.
Однако это не означает, что все информационные элементы,
присутствующие в S, обязательно будут присутствовать и
в Sf, часть из них может отсутствовать, если
таких ключевых слов нет в анализируемом тексте.
Сумма всех коэффициентов как для множества S, так и для множества Sf должна равняться единице.
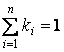 , n = | I |. , n = | I |.
 , n = | If |. , n = | If |.
Если это условие изначально не выполняется, а это может быть
связано с особенностями алгоритмической реализации выделения тематики,
необходимо привести эти суммы к единице (нормировать по 1).
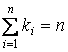 , ,  . .
Аналогично для kfi.
После этого можно вычислять тематическую близость по каждому
из информационных элементов.
Традиционно в информационно-поисковых системах, реализующих
векторную модель поиска, для вычисления меры близости векторов используется
косинус угла, определяемый через скалярное произведение векторов [8]:
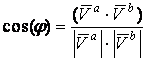 , ,
где: 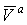 и и
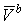 - сравниваемые вектора. - сравниваемые вектора.
В нашем случае использование такого подхода неприемлемо,
т.к.  определяет меру близости самих
векторов, а не их отдельных элементов. определяет меру близости самих
векторов, а не их отдельных элементов.
Тематическую близость 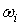 по каждому из информационных элементов
будем вычислять как: по каждому из информационных элементов
будем вычислять как:
 , ,
 , ,
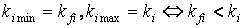 . .
Смысл этой формулы сводится к вычислению отношения между
весовыми коэффициентами, которое учитывает разницу (отличие) между ними.
Использование модуля разницы | ki – kfi | в качестве оценки
их отличия в данном случае не приемлемо, т.к. разница не чувствительна к малым
значениям коэффициентов kfi и ki, и отличие этих
коэффициентов при их малых значениях не будет заметно. В этом случае
использование отношения более корректно. В числителе этого отношения коэффициент
ki min, равный ki,
если ki < kfi и kfi,
если kfi < ki. Соответственно в знаменателе - оставшийся
коэффициент. Это необходимо для того, чтобы wi лежало в диапазоне от 0 до 1.
Множитель ki учитывает степень значимости данной разницы по отношению к
документу образцу, т.е. насколько значимо отличие коэффициентов для данного информационного
элемента в тематике текста образца.
Коэффициент общей тематической близости для всего текста, будет вычисляться как сумма всех
 : :
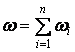 . .
При этом  будет принимать
значения в диапазоне от 0 до 1. будет принимать
значения в диапазоне от 0 до 1.
Вычисляя  для каждого
найденного документа (текста), можно выполнить ранжирование этих документов по тематической близости. для каждого
найденного документа (текста), можно выполнить ранжирование этих документов по тематической близости.
Учет контекста. Рассмотренный выше способ расчета тематической близости необходимо
дополнить одним важным соображением.
Как уже было сказано выше, значение слова определяется по его
контексту, по тем словам, которые употреблялись вместе с ним. Особенно это
значимо при вычислении тематической близости.
Одно и то же слово, присутствующее в S
и Sf, может нести в себе совершенно разный
смысловой оттенок, смысловую нагрузку. И простого сравнения весовых
коэффициентов недостаточно для корректного вычисления тематической близости.
Существует два традиционных подхода, позволяющих учесть
значение контекста. Первый использует предварительно сформированные тезаурусы –
словари, описывающие понятия языка и определяющие семантические отношениями
между ними. В таких словарях могут задаваться тематические категории слов, их
синонимы, анонимы, ассоциативные связи и др. [13, 86, 22], а также онтологии –
спецификации предметной области [69]. Второй подход предполагает анализ
коллекции доступных документов и уточнение метрик близости с учетом реального
содержимого коллекций [104, 112, 129, 113].
В данной работе предлагается способ учета контекста на базе
самого текста без дополнительного анализа документов коллекции и без
использования словарей.
Исходя из предложенной модели структурной организации
текста, при вычислении тематической близости необходимо выделять для каждого
ключевого слова (множество ключевых слов, определяющих тематику, уже определено
к этому моменту) контекст, т.е. слова входящие в окрестность данного слова. И
затем учитывать контекст при сравнении ключевых слов различных текстов, т.е. сравнивать
контекст, в котором это слово использовалось в тексте-образце и тексте,
анализируемом на тематическую близость.
Приступим к разработке способа вычисления контекстной
близости.
Контекстной близостью будем называть коэффициент,
учитывающий отличие контекстов некоторого заданного слова для двух разных текстов.
Определение контекста, как было уже сказано выше,
выполняется относительно некоторого информационного элемента i,
являющегося ключевым элементом текста образца и текста, анализируемого на
тематическую близость 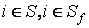 . .
S – множество ключевых элементов текста образца;
Sf - множество ключевых элементов анализируемого текста;
F – информационный поток, описывающий текст образец;
Ff – информационный поток, описывающий анализируемый на тематическую близость
некоторый найденный текст (документ).
1. Для i выделяем множество информационных элементов, входящих в его окрестность
(отдельно для F и Ff).
Это выполняется следующим образом:
Выделяем множество всех потоков, проходящих через
информационный элемент 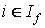 в некоторой окрестности заданной r. в некоторой окрестности заданной r.
A = D(F, i, [r-, r+]),
r- = r; r+ = r.
A = D(F, i, [r, r]).
Теперь из набора информационных элементов A
выделяем множество информационных элементов I:
A 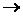 I, I,
I = {i1, i2, ..., in}.
Потом, все то же самое для потока Ff:
A = D(Ff, i, [r, r]),
A 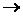 If, If,
If = {i1, i2, ..., in}.
В итоге имеем два множества I и If, определяющих
соответственно окрестность информационного элемента i текста образца и текста, анализируемого на тематическую
близость.
Приведенный выше порядок выделения окрестности идентичен, по
сути, рассмотренному выше контекстному анализу (параграф 2.2.). За тем лишь
исключением, что в данном случае нас не интересует количество повторений
информационных элементов в наборе A. Нас интересуют
только сам факт наличия или отсутствия информационных элементов в окрестности
элемента i.
2. Сравниваем окрестности и вычисляем коэффициент контекстной
близости.
Обозначим коэффициент контекстной близости - 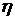 : :
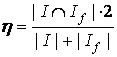
Очевидно, что 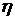 лежит в диапазоне от 0 до 1. лежит в диапазоне от 0 до 1.
1 – наибольшая и 0 – наименьшая степень близости.
Вычисление тематической близости с учетом контекста
перепишем в следующем виде:

Учитывая все вышеприведенные соображения относительно
контекста, кратко сформулируем основные пункты рассмотренного выше алгоритма.
1. Приведение суммы весов S и Sf к единице.
S – множество ключевых элементов текста образца;
Sf – множество ключевых элементов текста анализируемого на тематическую близость.
2. Вычисление тематической близости по весовым коэффициентам:
 , ,
 , ,
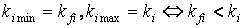 , ,
 . .
3. Вычисление контекстной близости по каждому ключевому элементу множества S:
 , ,
где:
I – множество информационных элементов входящих в окрестность информационного элемента i текста образца;
If – множество информационных элементов входящих в окрестность информационного элемента i анализируемого текста.
4. Вычисление общей тематической близости по всему тексту:
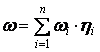 . .
Вычисление тематической близости текстов предполагает
предварительное выделение ключевых слов этих текстов с некоторыми весами и
последующее их сравнение между собой, т.е. вычисление меры их близости. Сами тексты
при этом не сравниваются, речь идет о переносе оценки тематической близости
ключевых слов на весь текст. Эта традиционный, общепринятый подход, применяемый
в подавляющем большинстве поисковых систем.
Сравниваются не сами тексты, а их приближенное представление
в виде тематики. Очевидна при этом условность такого сравнения, и значительное
влияние на результат сравнения параметров, используемых при выделении тематики.
Соответственно, получаемые значения тематической близости могут в значительной
мере отличаться.
Кроме того, необходимо отметить исключительную
субъективность самого понятия тематической близости текстов. Это понятие
предполагает значительную роль и участие человека в оценке тематической
близости текстов. У человека есть некоторые ожидания относительно искомых текстов
(документов) и их соответствия тексту-образцу. Предполагаемая человеком оценка
может в значительной мере отличаться от вычисленной оценки приближенного
представления текстов.
Для корректного вычисления тематической близости необходимо
учитывать как параметры, использованные при выделении тематики, так и
субъективную составляющую. Это предполагает реализацию некоторого варианта
предварительной настройки для того, чтобы получаемые в результате вычислений
значения соответствовали ожиданиям пользователя.
Традиционно, реализация такой настройки осуществляется на
основе информации обратной связи [36, 39], получаемой от пользователя.
Использование обратной связи для настройки некоторых
параметров методов тематического анализа или уточнения пользовательского
запроса не является чем-то принципиально новым, однако реализация подобной идеи
применительно к решению задачи подбора оптимальных параметров для выделения
тематики текста, с учетом экспертных оценок, автору не встречалась. Отсутствие
каких либо доступных способов решения этой задачи обуславливает необходимость
их разработки.
Приступим к разработке алгоритма поиска оптимальных
параметров выделения тематики. Эти параметры назовем информационными признаками
тематики.
Обозначим:
Т – текст;
S – тематика текста (множество ключевых слов);
F - функция используемая для перехода от T к S (метод частотно-контекстной классификации).
На рис. 2.5. приведена общая схема тематического представления текста.

Рис. 2.5. Тематическое представление документов
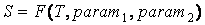 , ,
где: param1,
param2 – параметры, используемые при
выделении тематики.
- param1 - порог, используемый для выделения первичного множества ключевых слов.
- param2 - расстояние r, задающее окрестность, в пределах которой анализируются информационные потоки.
Задача состоит в том, чтобы определить оптимальные величины
этих параметров, позволяющие получить вычисленную оценку тематической близости
(на основе выделения тематики с данными параметрами), наиболее близкую к оцененной
тематической близости, т.е. найти значения информационных признаков тематики.
Очевидно, что определить эти параметры можно только на
основе экспертных оценок тематической близости самих текстов, т.е. учитывая
субъективную составляющую, учитывая ожидания эксперта. В данном контексте
эксперт – это пользователь поисковой системы. Совсем не обязательно при этом,
что он имеет какие-то априорные знания по теме искомых текстов (документов).
Эта оценка необходима, чтобы учесть его ожидания, учесть его критерии оценки
тематической близости.
Обозначим:
L – функция определяющая тематическую близость;
Le(T1, T2) – функция реализуемая самим человеком, при
определении тематической близости двух текстов;
Lс(S1, S2) – функция реализуемая поисковый системой
при вычислении тематической близости двух множеств ключевых слов определяющих
тематику текстов.
Допустим, что результатом вычисления этих функций являются
два коэффициента тематической близости:
Le(T1, T2) = ke,
Lс(S1, S2) = kc.
ke и kc лежат в диапазоне от 0 до 1.
Погрешность оценки тематической близости p,
полученная в результате вычислений, по отношению к экспертной оценке может быть
записана как разница коэффициентов:
p = | ke - kc |.
В процентах:
 . .
Смысл этого выражения в том, чтобы определить, на сколько
отличается коэффициент тематической близости, полученный в результате
вычислений от оценки эксперта. Оценка эксперта в данном случае выступает в
качестве эталона.
Теперь приступим к разработке алгоритма поиска значений информационных признаков тематики.
Пусть существует три разных текста:
T1 – текст образец;
T2, T3 – тексты анализируемые на тематическую близость к T1.
Для каждого из этих текстов существует их приближенное
представление в виде набора ключевых слов:
 , ,
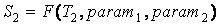 , ,
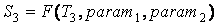 . .
S1, S2, S3 – тематические представления текстов
T1, T2, T3, полученные при некоторых идентичных параметрах функции F.
Пусть имеются оценки тематической близости:
Le(T1, T2) = ke1,
Le(T1, T3) = ke2,
Lc(S1, S2) = kc1,
Lc(S1, S3) = kc2,
Тогда, для оптимальных параметров F, будет выполняться условие:
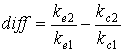 , ,
diff = 0.
Для того, чтобы подобрать оптимальные параметры, необходимо для каждой комбинации параметров получить
свои S1, S2, S3, затем вычислить для них тематическую близость
kc1 и kc2, подставить в diff и вычислить его значение.
Минимальное абсолютное значение diff, полученное для некоторой комбинации параметров, будет
соответствовать наиболее оптимальным параметрам (optimal) для данного метода тематической классификации:
 |
(2.1) |
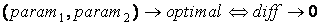 |
(2.2) |
Самый простой вариант подбора параметров – это перебор всех
возможных комбинаций параметров и нахождение минимального diff.
Разумным вариантом представляется использование одного из метода прямого поиска
минимума функций, например метода Хука-Дживса, позволяющего значительно
сократить вычислительные ресурсы и время поиска.
Смысл условия (2.2) состоит в том, что для метода выделения
тематики текста подбираются такие параметры, которые позволяют затем получать,
оценки наиболее близкие к оценкам, ожидаемым экспертом, а точнее, получать
близкие соотношения оценок по некоторым заданным текстам.
Чтобы привести вычисленную оценку к оценочной шкале эксперта,
необходимо ввести масштабирующий коэффициент:
 |
(2.3) |
Коэффициент вычисляется как среднее арифметическое по двум
отношениям, т.к. пользователь дважды оценивал тексты.
Этот коэффициент учитывает соотношение между оценкой
эксперта и вычисленной оценкой при оптимально подобранных параметрах.
Тогда приведенная оценка будет вычисляться как:
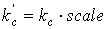 . .
Используя обозначение коэффициента тематической близости (параграф 2.3), приведенную оценку можно
записать через  : :
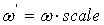 . .
Необходимо отметить один важный момент: корректно говорить о
подборе оптимальных параметров можно лишь для некоторого множества текстов, в
нашем случае это T1, T2, T3.
Гарантировать оптимальность найденных параметров для всех
последующих текстов, сравниваемых с текстом-образцом, невозможно. Подобранные
параметры и масштабирующий коэффициент будут давать гарантированный результат
(с некоторой ошибкой, определяемой diff) только для
проверенных текстов. Относительно других текстов, которые будут затем
анализироваться в автоматическом режиме, без экспертной оценки их тематической
близости можно лишь предположить, что найденные параметры и масштабирующий
коэффициент будут давать близкие результаты к ранее найденным соотношениям.
Если пользователь в процессе работы изменит свои субъективные критерии
тематической близости, то система (реализующая данный алгоритм) должна
пересчитать параметры и масштабирующий коэффициент, т.е. по ходу поиска, в
случае несоответствия ожидаемой оценки – вычисленной оценке, пользователь
должен уточнить свои экспертные оценки относительно вновь просматриваемых текстов.
Существует также возможность экспертной оценки по некоторому
произвольному числу текстов с подбором оптимальных параметров для серии
оцененных пользователем документов. Детальное рассмотрение этого вопроса
требует дополнительной теоретической проработки и экспериментальных
исследований.
Кроме того, необходимо отметить зависимость получаемых
результатов от адекватности и последовательности выставляемых экспертом оценок.
Если эксперт оценивает совершенно идентичные тексты по-разному, произвольно
меняя свои критерии оценки, то система, реализующая данный алгоритм, не сможет
корректно отработать эти оценки, т.е. найти оптимальные параметры для выделения
тематики и масштабирующий коэффициент, удовлетворяющий заданным соотношениям.
Результат в этом случае не определен.
Кратко сформулируем основные пункты рассмотренного выше алгоритма.
Существует три разных текста:
T1 – текст образец
T2, T3 – тексты анализируемые на тематическую близость к T1.
Существует экспертная оценка тематической близости этих текстов:
Le(T1, T2) = ke1,
Le(T1, T3) = ke2.
Существует множество комбинаций параметров используемых при
выделении, их тематики:
PARAM = {(param1, param2)1, ..., (param1, param2)n},
где: n – число комбинаций параметров
1. Для каждого текста выделить тематику с идентично заданными параметрами:
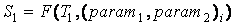 , ,
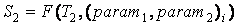 , ,
 . .
2. Вычислить тематическую близость:
Lc(S1, S2) = kc1,
Lc(S1, S3) = kc2.
3. Вычислить разницу отношений между экспертными и вычисленными оценками:

4. Повторяя пункты 1,2,3, определить минимальную разницу diff, для некоторой комбинации параметров,
которая и будет оптимальной.
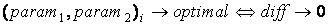 . .
5. Вычислить масштабирующий коэффициент:

В данной главе были разработаны:
- графовая модель структурного представления текста произвольного содержания;
- метод частотно-контекстной классификации тематики текста;
- алгоритм вычисления степени тематической принадлежности текста к образцу;
- алгоритм поиска значений информационных признаков тематики текста.
1. Графовая модель структурного представления текста
произвольного содержания позволяет отобразить семантическую связность и
последовательность текста в виде структуры.
Достоинства структурного представления:
- позволяет наглядно представить и выявить некоторые нетривиальные зависимости и закономерности в тексте;
- значительно сокращает вычислительные ресурсы на поиск таких закономерностей;
- позволяет организовывать анализируемые тексты в единую, целостную информационную структуру,
обеспечивая последующий анализ совокупности документов и выделение из них общих тематических кластеров.
2. Метод частотно-контекстной классификации тематики текста,
позволяет выделять тематику текста в виде множества ключевых слов с весами, характеризующими
значимость данных слов в тематике.
Достоинством метода является меньшая чувствительность к
частотным выбросам частотно-значимых слов, т.к. выделение тематики не
ограничивается одним лишь выделением этих слов. Преимущество метода – в дополнении
первичного набора ключевых элементов (сформированных на основе частотно-значимых
слов) контекстом, что позволяет точнее отобразить тематику текста.
3. Алгоритм вычисления степени тематической принадлежности
текста к образцу позволяет получать количественную оценку тематической близости
текстов. Достоинством алгоритма является использование контекстного анализа
при вычислении тематической близости совпадающих ключевых слов различных текстов.
Такой анализ позволяет учесть системную организацию текста, учесть не только ключевые
слова текста, определяющие его тематику, но и их совокупную связь с другими
словами, формирующими контекст этих слов. Это позволяет учесть значение слова в
контексте всего текста, сравнивая ключевые слова (двух разных текстов) не только
по их весам, но и по их контексту, учитывая смысловые отличия одних и тех же
слов для разных текстов.
4. Алгоритм поиска значений информационных признаков
тематики текста позволяет учесть субъективный характер оценки тематической
близости текста и настроить систему, реализующую поиск текстов по образцу под
конкретного пользователя, учесть его ожидания и представления относительно
тематической близости текстов.
Перспективным направлением исследований представляется поиск
тематически близких документов на основе подобия их структуры, т.е. выявлении
общих структурных особенностей текстов, удовлетворяющих информационным
потребностям пользователя. Сейчас выделение тематики предполагает анализ
структуры текста и оформление результатов анализа в виде векторной модели для
последующего поиска документов на основе этой модели.
|
 материалы
материалы  справочник
справочник  форум
форум  гостевая
гостевая  ссылки
ссылки