|
Для работы с словарем требуются поиск, вставка и удаление. Один из наиболее эффективных способов реализации
словаря – хеш-таблицы. Среднее время поиска элемента в них есть O(1), время для наихудшего случая – O(n).
Прекрасное изложение хеширования можно найти в работах Кормена[2] и Кнута[1]. Чтобы читать статьи на эту тему,
вам понадобится владеть соответствующей терминологией. Здесь описан метод, известный как связывание или открытое
хеширование[3]. Другой метод, известный как замкнутое хеширование[3] и адресация[1], здесь не
обсуждаются. Ну, как?
Теория
Хеш-таблица – это обычный массив с необычной адресацией, задаваемой хеш-функцией. Например, на hashTable
рис. 3.1 – это массив из 8 элементов. Каждый элемент представляет собой указатель на линейный список, хранящий
числа. Хеш-функция в этом примере просто делит ключ на 8 и использует остаток как индекс в таблице. Это дает
нам числа от 0 до 7 Поскольку для адресации в hashTable нам и нужны числа от 0 до 7, алгоритм гарантирует
допустимые значения индексов.
 |
Рис. 3.1. Хеш-таблица |
Чтобы вставить в таблицу новый элемент, мы хешируем ключ, чтобы определить список, в который его нужно
добавить, затем вставляем элемент в начало этого списка. Например, чтобы добавить 11, мы делим 11 на 8 и
получаем остаток 3. Таким образом, 11 следует разместить в списке, на начало которого указывает hashTable[3].
Чтобы найти число, мы его хешируем и проходим по соответствующему списку. Чтобы удалить число, мы находим
его и удаляем элемент списка, его содержащий.
Если хеш-функция распределяет совокупность возможных ключей равномерно по множеству индексов, то
хеширование эффективно разбивает множество ключей. Наихудший случай – когда все ключи хешируются в один
индекс. При этом мы работаем с одним линейным списком, который и вынуждены последовательно сканировать каждый
раз, когда что-нибудь делаем. Отсюда видно, как важна хорошая хеш-функция. Здесь мы рассмотрим лишь
несколько из возможных подходов. При иллюстрации методов предполагается, что unsigned char располагается в
8 байтах, unsigned short int – в 16, unsigned long int – в 32.
- Деление (размер таблицы hashTableSize – простое число). Этот метод использован в последнем
примере. Хеширующее значение hashValue, изменяющееся от 0 до (hashTableSize - 1), равно остатку от
деления ключа на размер хеш-таблицы. Вот как это может выглядеть:
typedef int hashIndexType;
hashIndexType hash(int Key) {
return Key % hashTableSize;
}
|
Для успеха этого метода очень важен выбор подходящего значения hashTableSize. Если, например,
hashTableSize равняется двум, то для четных ключей хеш-значения будут четными, для нечетных – нечетными.
Ясно, что это нежелательно – ведь если все ключи окажутся четными, они попадут в один элемент таблицы.
Аналогично, если все ключи окажутся четными, то hashTableSize, равное степени двух, попросту возьмет часть
битов Key в качестве индекса. Чтобы получить более случайное распределение ключей, в качестве hashTableSize
нужно брать простое число, не слишком близкое к степени двух.
- Мультипликативный метод (размер таблицы hashTableSize есть степень 2n). Значение
Key умножается на константу, затем от результата берется необходимое число битов. В качестве такой
константы Кнут[1] рекомендует золотое сечение (sqrt(5) - 1)/2 = 0.6180339887499. Пусть, например, мы
работаем с байтами. Умножив золотое сечение на 28, получаем 158. Перемножим 8-битовый ключ и 158, получаем
16-битовое целое. Для таблицы длиной 25 в качестве хеширующего значения берем 5 младших битов младшего слова,
содержащего такое произведение. Вот как можно реализовать этот метод:
typedef unsigned char hashIndexType;
static const hashIndexType K = 158;
typedef unsigned short int hashIndexType;
static const hashIndexType K = 40503;
typedef unsigned long int hashIndexType;
static const hashIndexType K = 2654435769;
static const int S = w - m;
hashIndexType hashValue = (hashIndexType)(K * Key) >> S;
|
Пусть, например, размер таблицы hashTableSize равен 1024 (210). Тогда нам достаточен 16-битный индекс и S
будет присвоено значение 16 – 10 = 6. В итоге получаем:
typedef unsigned short int hashIndexType;
hashIndexType hash(int Key) {
static const hashIndexType K = 40503;
static const int S = 6;
return (hashIndexType)(K * Key) >> S;
}
|
- Аддитивный метод для строк переменной длины (размер таблицы равен 256). Для строк переменной
длины вполне разумные результаты дает сложение по модулю 256. В этом случае результат hashValue заключен между
0 и 244.
typedef unsigned char hashIndexType;
hashIndexType hash(char *str) {
hashIndexType h = 0;
while (*str) h += *str++;
return h;
}
|
- Исключающее ИЛИ для строк переменной длины (размер таблицы равен 256). Этот метод аналогичен
аддитивному, но успешно различает схожие слова и анаграммы (аддитивный метод даст одно значение для XY и YX).
Метод, как легко догадаться, заключается в том, что к элементам строки последовательно применяется операция
“исключающее или”. В нижеследующем алгоритме добавляется случайная компонента, чтобы еще улучшить результат.
typedef unsigned char hashIndexType;
unsigned char Rand8[256];
hashIndexType hash(char *str) {
unsigned char h = 0;
while (*str) h = Rand8[h ^ *str++];
return h;
}
|
Здесь Rand8 – таблица из 256 восьмибитовых случайных чисел. Их точный порядок не критичен. Корни этого
метода лежат в криптографии; он оказался вполне эффективным [4].
- Исключающее ИЛИ для строк переменной длины (размер таблицы Ј 65536).
Если мы хешируем строку дважды, мы получим хеш-значение для таблицы любой длины до 65536. Когда строка
хешируется во второй раз, к первому символу прибавляется 1. Получаемые два 8-битовых числа объединяются в
одно 16-битовое.
typedef unsigned short int hashIndexType;
unsigned char Rand8[256];
hashIndexType hash(char *str) {
hashIndexType h;
unsigned char h1, h2;
if (*str == 0) return 0;
h1 = *str; h2 = *str + 1;
str++;
while (*str) {
h1 = Rand8[h1 ^ *str];
h2 = Rand8[h2 ^ *str];
str++;
}
h = ((hashIndexType)h1 << 8)|(hashIndexType)h2;
return h % hashTableSize
}
|
Размер хеш-таблицы должен быть достаточно велик, чтобы в ней оставалось разумное число пустых мест.
Как видно из таблицы 3.1, чем меньше таблица, тем больше среднее время поиска ключа в ней. Хеш-таблицу
можно рассматривать как совокупность связанных списков. По мере того, как таблица растет, увеличивается
количество списков и, соответственно, среднее число узлов в каждом списке уменьшается. Пусть количество
элементов равно n. Если размер таблицы равен 1, то таблица вырождается в один список длины n. Если размер
таблицы равен 2 и хеширование идеально, то нам придется иметь дело с двумя списками по n/100 элементов в
каждом. Как мы видим в таблице 3.1, имеется значительная свободы в выборе длины таблицы.
| size | time | size | time |
| 1 | 869 | 128 | 9 |
| 2 | 432 | 256 | 6 |
| 4 | 214 | 512 | 4 |
| 8 | 106 | 1024 | 4 |
| 16 | 54 | 2048 | 3 |
| 32 | 28 | 4096 | 3 |
| 64 |
15 |
8192 |
3 |
Таблица 3.1. Зависимость среднего времени поиска (ms) от
hashTableSize.
Сортируются 4096 элементов. |
Реализация
Реализация алгоритма на Си находится в разделе 4.5. Операторы typedef T и compGT следует изменить
так, чтобы они соответствовали данным, хранимым в массиве. Для работы программы следует также определить
hashTableSize и отвести место под hashTable. В хеш-функции hash использован метод деления.
Функция insertNode отводит память под новый узел и вставляет его в таблицу. Функция deleteNode удаляет
узел и освобождает память, где он располагался. Функция findNode ищет в таблице заданный ключ.
В разделе 1 мы использовали двоичный поиск для поиска данных в массиве. Этот метод чрезвычайно эффективен,
поскольку каждая итерация вдвое уменьшает число элементов, среди которых нам нужно продолжать поиск. Однако,
поскольку данные хранятся в массиве, операции вставки и удаления элементов не столь эффективны. Двоичные деревья
позволяют сохранить эффективность всех трех операций – если работа идет с “случайными” данными. В этом случае
время поиска оценивается как O(lg n). Наихудший случай – когда вставляются упорядоченные данные. В этом случае
оценка время поиска – O(n). Подробности вы найдете в работе Кормена [2].
Теория
Двоичное дерево – это дерево, у которого каждый узел имеет не более двух наследников. Пример бинарного дерева
приведен на рис. 3.2. Предполагая, что Key содержит значение, хранимое в данном узле, мы можем сказать, что
бинарное дерево обладает следующим свойством: у всех узлов, расположенных слева от данного узла, значение
соответствующего поля меньше, чем Key, у всех узлов, расположенных справа от него, – больше. Вершину дерева
называют его корнем, узлы, у которых отсутствуют оба наследника, называются листьями. Корень дерева на рис. 3.2
содержит 20, а листья – 4, 16, 37 и 43. Высота дерева – это длина наидлиннейшего из путей от корня к листьям. В
нашем примере высота дерева равна 2.
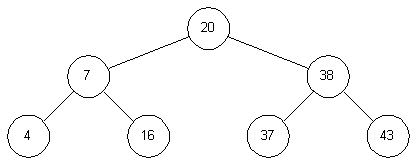 |
Рис. 3.2. Двоичное дерево |
Чтобы найти в дереве какое-то значение, мы стартуем из корня и движемся вниз. Например, для поиска числа 15,
мы замечаем, что 16 < 20, и потому идем влево. При втором сравнении имеем 16 > 7, так что мы движемся вправо.
Третья попытка успешна – мы находим элемент с ключом, равным 15.
Каждое сравнение вдвое уменьшает количество оставшихся элементов. В этом отношении алгоритм похож на двоичный
поиск в массиве. Однако, все это верно только в случаях, когда наше дерево сбалансировано. На рис. 3.3 показано
другое дерево, содержащее те же элементы. Несмотря на то, что это дерево тоже бинарное, поиск в нем похож, скорее,
на поиск в односвязном списке, время поиска увеличивается пропорционально числу запоминаемых элементов.
 |
Рис. 3.3. Несбалансированное бинарное дерево |
Вставка и удаление
Чтобы лучше понять, как дерево становится несбалансированным, посмотрим на процесс вставки пристальнее. Чтобы
вставить 18 в дерево на рис. 3.2 мы ищем это число. Поиск приводит нас в узел 16, где благополучно завершается.
Поскольку 18 > 16, мы попросту добавляет узел 18 в качестве правого потомка узла 16 (рис. 3.4).
Теперь мы видим, как возникает несбалансированность дерева. Если данные поступают в возрастающем порядке, каждый
новый узел добавляется справа от последнего вставленного. Это приводит к одному длинному списку. Обратите внимание:
чем более “случайны” поступающие данные, тем более сбалансированным получается дерево.
Удаления производятся примерно так же – необходимо только позаботиться о сохранении структуры дерева. Например,
если из дерева на рис. 3.4 удаляется узел 20, его сначала нужно заменить на узел 37. Это даст дерево, изображенное
на рис. 3.5. Рассуждения здесь примерно следующие. Нам нужно найти потомка узла 20, справа от которого расположены
узлы с большими значениями. Таким образом, нам нужно выбрать узел с наименьшим значением, расположенный справа от
узла 20. Чтобы найти его, нам и нужно сначала спуститься на шаг вправо (попадаем в узел 38), а затем на шаг влево
(узел 37); эти двухшаговые спуски продолжаются, пока мы не придем в концевой узел, лист дерева.
 |
Рис. 3.4. Бинарное дерево после добавления узла 18 |
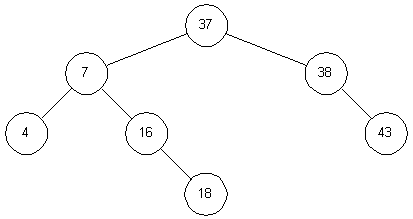 |
Рис. 3.5. Бинарное дерево после удаления узла 20 |
Реализация
Реализация алгоритма на Си находится в разделе 4.6. Операторы typedef T и compGT следует изменить так,
чтобы они соответствовали данным, хранимым в дереве. Каждый узел Node содержит также указатели left, right
на левого и правого потомков, а также указатель parent на предка. Собственно данные хранятся в поле data.
Адрес узла, являющегося корнем дерева хранится в укзателе root, значение которого в самом начале,
естественно, NULL. Функция insertNode запрашивает память под новый узел и вставляет узел в дерево, т.е.
устанавливает нужные значения нужных указателей. Функция deleteNode, напротив, удаляет узел из дерева (т.е.
устанавливает нужные значения нужных указателей), а затем освобождает память, которую занимал узел. Функция
findNode ищет в дереве узел, содержащий заданное значение.
Двоичные деревья работают лучше всего, когда они сбалансированы, когда длина пути от корня до любого из листьев
находится в определенных пределах, связанных с числом узлов. Красно-черные деревья – один из способов балансировки
деревьев. Название происходит от стандартной раскраски узлов таких деревьев в красный и черный цвета. Цвета узлов
используются при балансировке дерева. Во время операций вставки и удаления поддеревья может понадобиться повернуть,
чтобы достигнуть сбалансированности дерева. Оценкой как среднего время, так и наихудшего является O(lg n).
Этот раздел – один из наиболее трудных в данной книжке. Если вы ошалеете от вращений деревьев, попробуйте перейти
к следующему разделу о разделенных списках. Прекрасно написанные разделы о красно-черных деревьях вы найдете у
Кормена[2].
Теория
Красно-черное дерево – это бинарное дерево с следующими свойствами[2]:
- Каждый узел покрашен либо в черный, либо в красный цвет.
- Листьями объявляются NIL-узлы (т.е. “виртуальные” узлы, наследники узлов, которые обычно называют листьями;
на них “указывают” NULL указатели). Листья покрашены в черный цвет.
- Если узел красный, то оба его потомка черны.
- На всех ветвях дерева, ведущих от его корня к листьям, число черных узлов одинаково.
Количество черных узлов на ветви от корня до листа называется черной высотой дерева. Перечисленные свойства
гарантируют, что самая длинная ветвь от корня к листу не более чем вдвое длиннее любой другой ветви от корня к листу.
Чтобы понять, почему это так, рассмотрим дерево с черной высотой 2. Кратчайшее возможное расстояние от корня до
листа равно двум – когда оба узла черные. Длиннейшее расстояние от корня до листа равно четырем – узлы при этом
покрашены (от корня к листу) так: красный–>черный–>красный–>черный. Сюда нельзя добавить черные узлы, поскольку
при этом нарушится свойство 4, из которого вытекает корректность понятия черной высоты. Поскольку согласно свойству
3 у красных узлов непременно черные наследники, в подобной последовательности недопустимы и два красных узла
подряд. Таким образом, длиннейший путь, который мы можем сконструировать, состоит из чередования красных и черных
узлов, что и приводит нас к удвоенной длине пути, проходящего только через черные узлы. Все операции над деревом
должны уметь работать с перечисленными свойствами. В частности, при вставке и удалении эти свойства должны
сохраниться.
Вставка
Чтобы вставить узел, мы сначала ищем в дереве место, куда его следует добавить. Новый узел всегда добавляется
как лист, поэтому оба его потомка являются NIL-узлами и предполагаются черными. После вставки красим узел в красный
цвет. После этого смотрим на предка и проверяем, не нарушается ли красно-черное свойство. Если необходимо,
мы перекрашиваем узел и производим поворот, чтобы сбалансировать дерево.
Вставив красный узел, мы сохраняем свойство черной высоты (свойство 4). Однако, при этом может оказаться нарушенным
свойство 3. Это свойство состоит в том, что оба потомка красного узла обязательно черны. В нашем случае оба потомка
нового узла черны по определению (поскольку они являются NIL-узлами), так что рассмотрим ситуацию, когда предок
нового узла красный: при этом будет нарушено свойство 3. Достаточно рассмотреть следующие два случая:
- Красный предок, красный “дядя”. Ситуацию красный-красный иллюстрирует рис. 3.6. У нового узла X
предок и “дядя” оказались красными. Простое перекрашивание избавляет нас от красно-красного нарушения.
После перекраски нужно проверить “дедушку” нового узла (узел B), поскольку он может оказаться красным.
Обратите внимание на распространение влияния красного узла на верхние узлы дерева. В самом конце корень мы
красим в черный цвет корень дерева. Если он был красным, то при этом увеличивается черная высота дерева.
- Красный предок, черный “дядя”. На рис. 3.7 представлен другой вариант красно-красного нарушения
– “дядя” нового узла оказался черным. Здесь узлы может понадобиться вращать, чтобы скорректировать
поддеревья. В этом месте алгоритм может остановиться из-за отсутствия красно-красных конфликтов и вершина
дерева (узел A) окрашивается в черный цвет. Обратите внимание, что если узел X был в начале правым потомком,
то первым применяется левое вращение, которое делает этот узел левым потомком.
Каждая корректировка, производимая при вставке узла, заставляет нас подняться в дереве на один шаг. В этом
случае до остановки алгоритма будет сделано 1 вращение (2, если узел был правым потомком). Метод удаления
аналогичен.
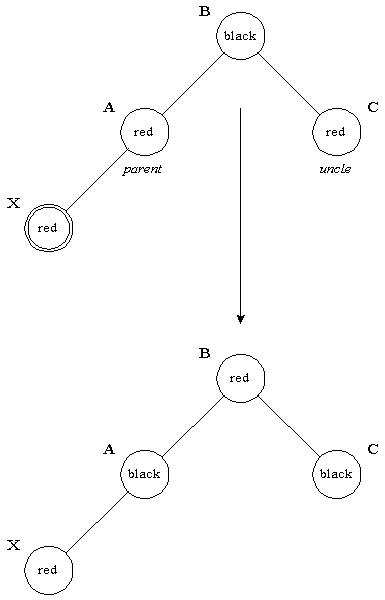 |
Рис. 3.6. Вставка – Красный предок, красный “дядя” |
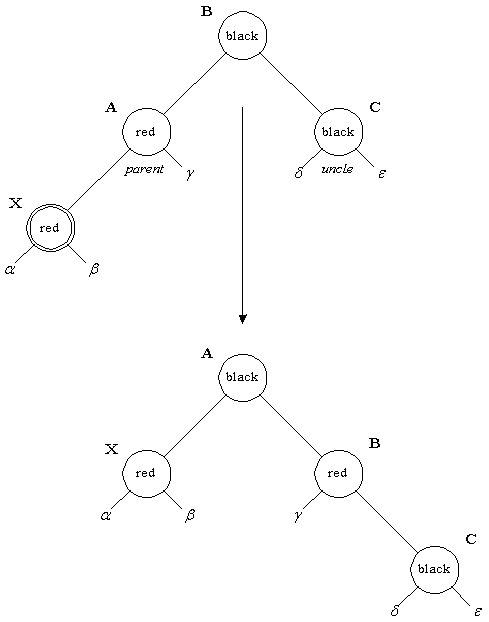 |
Рис. 3.7. Вставка – красный предок, черный “дядя” |
Реализация
Реализация работы с красно-черными деревьями на Си находится в разделе 4.7. Операторы typedef T, а
также сравнивающие compLT и compEQ следует изменить так, чтобы они соответствовали данным, хранимым в
узлах дерева. В каждом узле Node хранятся указатели left, right на двух потомков и parent на предка.
Цвет узла хранится в поле color и может быть либо RED, либо BLACK. Собственно данные хранятся в поле
data. Все листья дерева являются “сторожевыми” (sentinel), что сильно упрощает коды. Узел root
является корнем дерева и в самом начале является сторожевым.
Функция insertNode запрашивает память под новый узел, устанавливает нужные значения его полей и вставляет
в дерево. Соответственно, она вызывает insertFixup, которая следит за сохранением красно-черных свойств.
Функция deleteNode удаляет узел из дерева. Она вызывает deleteFixup, которая восстанавливает красно-черные
свойства. Функция findNode ищет в дереве нужный узел.
Разделенные списки – это связные списки, которые позволяют вам прыгнуть (skip) к нужному элементу.
Это позволяет преодолеть ограничения последовательного поиска, являющегося основным источником неэффективного
поиска в списках. В то же время вставка и удаление остаются сравнительно эффективными. Оценка среднего времени
поиска в таких списках есть O(lg n). Для наихудшего случая оценкой является O(n), но худший случай крайне
маловероятен. Отличное введение в разделенные списки вы найдете у Пью [5].
Теория
Идея, лежащая в основе разделенных списков, очень напоминает метод, используемый при поиске имен в адресной
книжке. Чтобы найти имя, вы помечаете буквой страницу, откуда начинаются имена, начинающиеся с этой буквы.
На рис. 3.8, например, самый верхний список представляет обычный односвязный список. Добавив один “уровень” ссылок,
мы ускорим поиск. Сначала мы пойдем по ссылкам уровня 1, затем, когда дойдем по нужного отрезка списка, пойдем по
ссылкам нулевого уровня.
Эта простая идея может быть расширена – мы можем добавить нужное число уровней. Внизу на рис. 3.8 мы видим второй
уровень, который позволяет двигаться еще быстрее первого. При поиске элемента мы двигаемся по этому уровню, пока не
дойдем до нужного отрезка списка. Затем мы еще уменьшаем интервал неопределенности, двигаясь по ссылкам 1-го уровня.
Лишь после этого мы проходим по ссылкам 0-го уровня.
Вставляя узел, нам понадобится определить количество исходящих от него ссылок. Эта проблема легче всего решается
с использованием случайного механизма: при добавлении нового узла мы “бросаем монету”, чтобы определить, нужно ли
добавлять еще слой. Например, мы можем добавлять очередные слои до тех пор, пока выпадает “решка”. Если реализован
только один уровень, мы имеем дело фактически с обычным списком и время поиска есть O(n). Однако, если имеется
достаточное число уровней, разделенный список можно считать деревом с корнем на высшем уровне, а для дерева время
поиска есть O(lg n).
Поскольку реализация разделенных списков включает в себя случайный процесс, для времени поиска в них
устанавливаются вероятностные границы. При обычных условиях эти границы довольно узки. Например, когда мы
ищем элемент в списке из 1000 узлов, вероятность того, что время поиска окажется в 5 раз больше среднего,
можно оценить как 1 / 1,000,000,000,000,000,000[5].
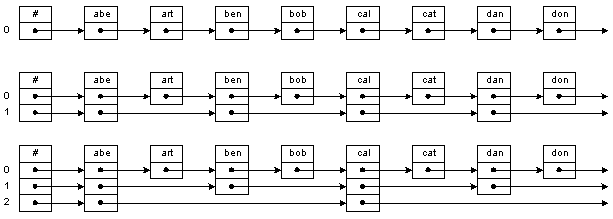 |
Рис. 3.8. Устройство разделенного списка |
Реализация
Реализация работы с разделенными списками на Си находится в разделе 4.8. Операторы typedef T, а
также compLT и compEQ следует изменить так, чтобы они соответствовали данным, хранимым в узлах списка.
Кроме того, понадобится выбрать константу MAXLEVEL; ее значение выбирается в зависимости от ожидаемого
объема данных.
Функция initList вызывается в самом начале. Она отводит память под заголовок списка и инициализирует
его поля. Признаком того, что список пуст, Функция insertNode создает новый узел и вставляет его в список.
Конечно, insertNode сначала отыскивает место в списке, куда узел должен быть вставлен. В массиве update
функция учитывает встретившиеся ссылки на узлы верхних уровней. Эта информация в дальнейшем используется
для корректной установки ссылок нового узла. Для этого узла, с помощью генератора случайных чисел,
определяется значение newLevel, после чего отводится память для узла. Ссылки вперед устанавливаются по
информации, содержащей в массиве update. Функция deleteNode удаляет узлы из списка и освобождает занимаемую
ими память. Она реализована аналогично функции findNode и так же ищет в списке удаляемый узел.
Мы рассмотрели несколько методов организации словарей: хеш-таблицы, несбалансированные двоичные деревья,
красно-черные деревья и разделенные списки. Имеются несколько факторов, которые влияют на выбор алгоритма
в конкретной ситуации:
- Сортировка результата. Если результат должен быть отсортирован, хеш-таблицы представляются не вполне
подходящими, поскольку их элементы заносятся в таблицу в порядке, определяемом только их хеш-значениями.
Все обстоит совсем по-другому при работе с двоичными деревьями. При проходе дерева в обратном порядке
(Терминология Д.Кнута (т.1,п.2.3.1): postorder. В оригинале данной работы этот же порядок назван in-order)
мы получаем отсортированный список. Вот как это делается:
void WalkTree(Node *P) {
if (P == NIL) return;
WalkTree(P->Left);
WalkTree(P->Right);
}
WalkTree(Root);
|
- Чтобы получить отсортированный список узлов разделенного списка, достаточно пройтись по ссылкам нулевого
уровня. Вот так:
Node *P = List.Hdr->Forward[0];
while (P != NIL) {
P = P->Forward[0];
}
|
- Память. Минимизация памяти, которая уходит на “накладные расходы”, особенно важна, когда нужно
хранить много маленьких узлов.
- Для хеш-таблиц требуется только один указатель на узел. Кроме того, требуется память под саму таблицу.
- Для красно-черных деревьев в каждом узле нужно хранить ссылку на левого и правого потомка, а также
ссылку на предка. Кроме того, где-то нужно хранить и цвет узла! Хотя на цвет достаточен только один бит,
из-за выравнивания структур, требуемого для эффективности доступа, как правило, будет потрачено больше
места. Таким образом, каждый узел красно-черного дерева требует памяти, которой хватило бы на 3-4
указателя.
- Для разделенных списков в каждом узле имеется ссылка нулевого уровня. Вероятность иметь ссылку
уровня 1 равна S. Вероятность иметь ссылку уровня 2 равна j. В общем, количество ссылок на узел
равно
- Время. Алгоритм должен быть эффективным. Это особенно важно, когда ожидаются большие объемы
данных. В таблице 3.2 сравниваются времена поиска для каждого алгоритма. Обратите внимание на то, что
наихудшие случаи для хеш-таблиц и разделенных списков чрезвычайно маловероятны. Экспериментальные данные
описаны ниже.
- Простота. Если алгоритм короток и прост, при его реализации и/или использовании ошибки будут
допущены с меньшей вероятностью. Кроме того, это облегчает проблемы сопровождения программ. Количества
операторов, исполняемых в каждом алгоритме, также содержатся в таблице 3.2.
| метод | операторы | среднее время | время в худшем случае |
| хеш-таблицы | 26 | O(1) | O(n) |
| несбалансированные деревья | 41 | O(lg n) | O(n) |
| красно-черные деревья | 120 | O(lg n) | O(lg n) |
| разделенные списки | 55 | O(lg n) | O(n) |
Таблица 3.2. Сравнение алгоритмов ведения словарей |
В таблице 3.3 приведены времена, требуемые для вставки, поиска и удаления 65536 (216) случайных элементов. В
этих экспериментах размер хеш-таблицы равнялся10009, для разделенных списков допускалось до 16 уровней ссылок. Конечно, в
реальных ситуациях времена могут отличаться от приведенных здесь, однако, таблица дает достаточно информации для выбора
подходящего алгоритма.
| метод | вставка | поиск | удаление |
| хеш-таблицы | 18 | 8 | 10 |
| несбалансированные деревья | 37 | 17 | 26 |
| красно-черные деревья | 40 | 16 | 37 |
| разделенные списки | 48 | 31 | 35 |
Таблица 3.3. Среднее время (мсек) для 65536 случайных элементов |
В таблице 3.4 приведены средние времена поиска для двух случаев: случайных данных, и упорядоченных, значения которых
поступали в возрастающем порядке. Упорядоченные данные являются наихудшим случаем для несбалансированных деревьев,
поскольку дерево вырождается в обычный односвязный список. Приведены времена для “одиночного” поиска. Если бы нам
понадобилось найти все 65536 элементов, то красно-черныму дереву понадобилось бы 6 секунд, а несбалансированному –
около 1 часа.
| | Элементов | хеш-таблицы | несбалансированные
деревья | красно-черные
деревья | разделенные
списки |
| случайные данные | 16 | 4 | 3 | 2 | 5 |
| 256 | 3 | 4 | 4 | 9 |
| 4,096 | 3 | 7 | 6 | 12 |
| 65,536 | 8 | 17 | 16 | 31 |
| упорядоченные данные | 16 | 3 | 4 | 2 | 4 |
| 256 | 3 | 47 | 4 | 7 |
| 4,096 | 3 | 1,033 | 6 | 11 |
| 65,536 | 7 | 55,019 | 9 | 15 |
Таблица 3.4. Среднее время поиска (мсек) |
|
 материалы
материалы  справочник
справочник  форум
форум  гостевая
гостевая  ссылки
ссылки