Простейшая
нейронная сеть - ПЕРСЕПТРОН Розенблатта. Линейная разделимость и теорема об обучении
персептрона.
В этой и последующих лекциях мы приступаем к непосредственному
рассмотрению основных, описанных в литературе, моделей искусственных нейронных сетей и
решаемых ими задач. Исходным будет изложение ПЕРСЕПТРОНА - первой нейросетевой парадигмы,
доведенной до кибернетической реализации.
ПЕРСЕПТРОН Розенблатта.
Одной из первых искусственных
сетей, способных к перцепции (восприятию) и формированию реакции на воспринятый стимул,
явился PERCEPTRON Розенблатта (F.Rosenblatt, 1957). Персептрон рассматривался его автором
не как конкретное техническое вычислительное устройство, а как модель работы мозга. Нужно
заметить, что после нескольких десятилетий исследований современные работы по искусственным
нейронным сетям редко преследуют такую цель.

Рис. 4.1. Элементарный персептрон Розенблатта.
Простейший классический
персептрон содержит нейрободобные элементы трех типов (см. Рис. 4.1), назначение которых в
целом соответствует нейронам рефлекторной нейронной сети, рассмотренной в предыдущей
лекции. S-элементы формируют сетчатку сенсорных клеток, принимающих двоичные сигналы от
внешнего мира. Далее сигналы поступают в слой ассоциативных или A-элементов (для упрощения
изображения часть связей от входных S-клеток к A-клеткам не показана). Только
ассоциативные элементы, представляющие собой формальные нейроны, выполняют нелинейную
обработку информации и имеют изменяемые веса связей. R-элементы с фиксированными весами
формируют сигнал реакции персептрона на входной стимул.
Розенблатт называл такую нейронную сеть трехслойной, однако по
современной терминологии, используемой в этой книге, представленная сеть обычно называется
однослойной, так как имеет только один слой нейропроцессорных элементов.
Однослойный персептрон характеризуется матрицей синаптических связей W от S- к
A-элементам. Элемент матрицы  отвечает связи, ведущей от i-го S-элемента к j-му A-элементу.
отвечает связи, ведущей от i-го S-элемента к j-му A-элементу.
В Корнельской авиационной лаборатории была разработана
электротехническая модель персептрона MARK-1, которая содержала 8 выходных R-элементов и
512 A-элементов, которые можно было соединять в различных комбинациях. На этом персептроне
была проведена серия экспериментов по распознаванию букв алфавита и геометрических
образов.
В работах Розенблатта был сделано заключение о том, что нейронная сеть
рассмотренной архитектуры будет способна к воспроизведению любой логической функции,
однако, как было показано позднее М.Минским и С.Пейпертом (M.Minsky, S.Papert, 1969), этот
вывод оказался неточным. Были выявлены принципиальные неустранимые ограничения однослойных
персептронов, и в последствии стал в основном рассматриваться многослойный вариант
персептрона, в котором имеются несколько слоев процессорных элементов.
С сегодняшних позиций однослойный персептрон представляет скорее
исторический интерес, однако на его примере могут быть изучены основные понятия и простые
алгоритмы обучения нейронных сетей.
Теорема об обучении персептрона.
Обучение сети состоит в
подстройке весовых коэффициентов каждого нейрона. Пусть имеется набор пар векторов
(xa,
ya),
a = 1..p, называемый обучающей выборкой. Будем
называть нейронную сеть обученной на данной обучающей выборке, если при подаче на входы
сети каждого
вектора xa
на выходах всякий раз получается соответсвующий вектор
ya
Предложенный Ф.Розенблаттом
метод обучения состоит в итерационной подстройке матрицы весов, последовательно уменьшающей
ошибку в выходных векторах. Алгоритм включает несколько шагов:
| Шаг 0. |
Начальные значения весов всех
нейронов 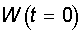 полагаются случайными. полагаются случайными.
|
| Шаг 1. |
Сети предъявляется входной образ
xa,
в результате формируется выходной образ

|
| Шаг 2. |
Вычисляется вектор ошибки
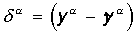 , делаемой сетью на выходе. Дальнейшая идея
состоит в том, что изменение
вектора весовых коэффициентов в области малых ошибок должно быть пропорционально ошибке
на выходе, и равно нулю если ошибка равна нулю. , делаемой сетью на выходе. Дальнейшая идея
состоит в том, что изменение
вектора весовых коэффициентов в области малых ошибок должно быть пропорционально ошибке
на выходе, и равно нулю если ошибка равна нулю.
|
| Шаг 3. |
Вектор весов модифицируется по
следующей формуле:  . Здесь . Здесь
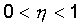 - темп
обучения. - темп
обучения.
|
| Шаг 4. |
Шаги 1-3 повторяются для всех
обучающих векторов. Один цикл последовательного предъявления всей выборки называется
эпохой. Обучение завершается по истечении нескольких эпох, а) когда итерации
сойдутся, т.е. вектор весов перестает измеяться, или б) когда полная просуммированная
по всем векторам абсолютная ошибка станет меньше некоторого малого значения.
|
Используемая на шаге 3
формула учитывает следующие обстоятельства: а) модифицируются только компоненты матрицы
весов, отвечающие ненулевым значениям входов; б) знак приращения веса соответствует знаку
ошибки, т.е. положительная ощибка (d > 0, значение выхода
меньше требуемого) проводит к усилению связи; в) обучение каждого
нейрона происходит независимо от обучения остальных нейронов, что соответсвует важному с
биологической точки зрения, принципу локальности обучения.
Данный метод обучения был назван Ф.Розенблаттом “методом коррекции с
обратной передачей сигнала ошибки”. Позднее более широко стало известно название “d
-правило”. Представленный алгоритм относится к широкому классу алгоритмов обучения с
учителем, поскольку известны как входные вектора, так и требуемые значения выходных
векторов (имеется учитель, способный оценить правильность ответа ученика).
Доказанная Розенблаттом
теорема о сходимости обучения по d
-правилу говорит о том, что персептрон способен обучится любому обучающему набору, который
он способен представить. Ниже мы более подробно обсудим возможности персептрона по
представлению информации.
Линейная разделимость и персептронная представляемость
Каждый нейрон персептрона
является формальным пороговым элементом, принимающим единичные значения в случае, если
суммарный взвешенный вход больше некоторого порогового значения:
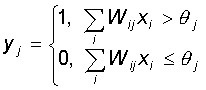
Таким образом, при заданных
значениях весов и порогов, нейрон имеет определенное значение выходной активности для
каждого возможного вектора входов. Множество входных векторов, при которых нейрон активен
(y=1), отделено от множества векторов, на которых нейрон пассивен (y=0)
гиперплоскостью, уравнение которой есть, суть:
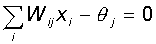
Следовательно, нейрон
способен отделить (иметь различный выход) только такие два множества векторов
входов, для которых имеется гиперплоскость, отсекающая одно множество от другого. Такие
множества называют линейно разделимыми. Проиллюстрируем это понятие на примере.
Пусть имеется нейрон, для которого входной вектор содержит только две
булевые компоненты 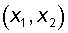 ,
определяющие плоскость. На данной
плоскости возможные значения векторов отвечают вершинам единичного квадрата. В каждой
вершине определено требуемое значение активности нейрона 0 (на рис. 4.2 - белая
точка) или 1 (черная точка). Требуется определить, существует ли такое такой набор весов и
порогов нейрона, при котором этот нейрон сможет отделить точки разного цвета? ,
определяющие плоскость. На данной
плоскости возможные значения векторов отвечают вершинам единичного квадрата. В каждой
вершине определено требуемое значение активности нейрона 0 (на рис. 4.2 - белая
точка) или 1 (черная точка). Требуется определить, существует ли такое такой набор весов и
порогов нейрона, при котором этот нейрон сможет отделить точки разного цвета?
На рис 4.2 представлена одна из ситуаций, когда этого сделать
нельзя вследствие линейной неразделимости множеств белых и черных точек.

Рис. 4.2. Белые точки не могут
быть отделены одной прямой от черных.
Требуемая активность нейрона
для этого рисунка определяется таблицей, в которой не трудно узнать задание логической
функции “ислючающее или”.
| X1 |
X2 |
Y |
| 0 |
0 |
0 |
| 1 |
0 |
1 |
| 0 |
1 |
1 |
| 1 |
1 |
0 |
Линейная неразделимость
множест аргументов, отвечающих различным значениям функции означает, что функция
“ислючающее или”, столь широко использующаяся в логических устройствах, не может быть
представлена формальным нейроном. Столь скромные возможности нейрона и послужили основой
для критики персептронного направления Ф.Розенблатта со стороны М.Минского и С.Пейперта.
При возрастании числа аргументов ситуация еще более катастрофична:
относительное число функций, которые обладают свойством линейной разделимости резко
уменьшается. А значит и резко сужается класс функций, который может быть реализован
персептроном (так называемый класс функций, обладающий свойством персептронной
представляемости). Соотвествующие данные приведены в следующей таблице:
| Число переменных N |
Полное число возможных логических
функций 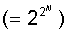 |
Из них линейно разделимых функций |
| 1 |
4 |
4 |
| 2 |
16 |
14 |
| 3 |
256 |
104 |
| 4 |
65536 |
1882 |
| 5 |
> 1000000000 |
94572 |
Видно, что однослойный
персептрон крайне ограничен в своих возможностях точно представить наперед заданную
логическую функцию. Нужно отметить, что позднее, в начале 70-х годов, это ограничение было
преодолено путем введения нескольких слоев нейронов, однако критическое отношение к
классическому персептрону сильно заморозило общий круг интереса и научных исследований в
области искусственных нейронных сетей.
В завершении остановимся на тех проблемах, которые остались открытыми
после работ Ф.Розенблатта. Часть из них была впоследствии решена (и будет частично
рассмотрена в следующих лекциях), некоторые остались без полного теоретического
решения.
- Практическая проверка
условия линейной разделимости множеств. Теорема Розенблатта гарантирует успешное обучение
только для персептронно представимых функций, однако ничего не говорит о том, как это
свойство практически обнаружить до обучения
- Сколько шагов потребуется
при итерационном обучении? Другими словами, затянувшееся обучение может быть как следсвием
не представимости функции (и в этом случае оно никогда не закончится), так и просто
особенностью алгоритма.
- Как влияет на обучение последовательность предъявления образов в
течение эпохи обучения?
- Имеет ли вообще d
-правило преимущества перед простым перебором весов, т.е. является ли оно конструктивным
алгоритмом быстрого обучения?
- Каким будет качество обучения, если обучающая выборка содержит не
все возможные пары векторов? Какими будут ответы персептрона на новые
вектора?
Последний вопрос затрагивает
глубокие пласты вычислительной нейронауки, касающиеся способностей искусственных систем к
обобщению ограничеснного индивидуального опыта на более широкий класс ситуаций, для
которых отклик был заранее не сообщен нейросети. Ситуация, когда системе приходится
работать с новыми образами, является типичной, так как число всех возможных примеров
экспоненциально быстро растет с ростом числа переменных, и поэтому на практике
индивидуальный опыт сети всегда принципиально не является полным.
Возможности обобщения в нейросетях будут подробнее рассмотрены на
следующей лекции.
|
 материалы
материалы  справочник
справочник  форум
форум  гостевая
гостевая  ссылки
ссылки