|
Введение
Стремительное развитие информационных технологий, в частности, прогресс в методах сбора, хранения и обработки данных позволил многим организациям собирать огромные массивы данных, которые необходимо анализировать. Объемы этих данных настолько велики, что возможностей экспертов уже не хватает, что породило спрос на методы автоматического исследования (анализа) данных, который с каждым годом постоянно увеличивается.
Деревья решений – один из таких методов автоматического анализа данных. Первые идеи создания деревьев решений восходят к работам Ховленда (Hoveland) и Ханта(Hunt) конца 50-х годов XX века. Однако, основополагающей работой, давшей импульс для развития этого направления, явилась книга Ханта (Hunt, E.B.), Мэрина (Marin J.) и Стоуна (Stone, P.J) «Experiments in Induction», увидевшая свет в 1966г.
Терминология
Введем основные понятия из теории деревьев решений, которые будут употребляться в этой и последующих статьях.
| Название |
Описание |
| Объект |
Пример, шаблон, наблюдение |
| Атрибут |
Признак, независимая переменная, свойство |
| Метка класса |
Зависимая переменная, целевая переменная, признак определяющий класс объекта |
| Узел |
Внутренний узел дерева, узел проверки |
| Лист |
Конечный узел дерева, узел решения |
| Проверка (test) |
Условие в узле |
Что такое дерево решений и типы решаемых задач
Деревья решений – это способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение.
Под правилом понимается логическая конструкция, представленная в виде «если … то …».

Область применения деревья решений в настоящее время широка, но все задачи, решаемые этим аппаратом могут быть объединены в следующие три класса:
- Описание данных: Деревья решений позволяют хранить информацию о данных в компактной форме, вместо них мы можем хранить дерево решений, которое содержит точное описание объектов.
- Классификация: Деревья решений отлично справляются с задачами классификации, т.е. отнесения объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные значения.
- Регрессия: Если целевая переменная имеет непрерывные значения, деревья решений позволяют установить зависимость целевой переменной от независимых(входных) переменных. Например, к этому классу относятся задачи численного прогнозирования(предсказания значений целевой переменной).
Как построить дерево решений?
Пусть нам задано некоторое обучающее множество T, содержащее объекты (примеры), каждый из которых характеризуется m атрибутами (атрибутами), причем один из них указывает на принадлежность объекта к определенному классу.
Идею построения деревьев решений из множества T, впервые высказанную Хантом, приведем по Р. Куинлену (R. Quinlan).
Пусть через {C1, C2, … Ck} обозначены классы(значения метки класса), тогда существуют 3 ситуации:
- множество T содержит один или более примеров, относящихся к одному классу Ck. Тогда дерево решений для Т – это лист, определяющий класс Ck;
- множество T не содержит ни одного примера, т.е. пустое множество. Тогда это снова лист, и класс, ассоциированный с листом, выбирается из другого множества отличного от T, скажем, из множества, ассоциированного с родителем;
- множество T содержит примеры, относящиеся к разным классам. В этом случае следует разбить множество T на некоторые подмножества. Для этого выбирается один из признаков, имеющий два и более отличных друг от друга значений O1, O2, … On. T разбивается на подмножества T1, T2, … Tn, где каждое подмножество Ti содержит все примеры, имеющие значение Oi для выбранного признака. Это процедура будет рекурсивно продолжаться до тех пор, пока конечное множество не будет состоять из примеров, относящихся к одному и тому же классу.
Вышеописанная процедура лежит в основе многих современных алгоритмов построения деревьев решений, этот метод известен еще под названием разделения и захвата (divide and conquer). Очевидно, что при использовании данной методики, построение дерева решений будет происходит сверху вниз.
Поскольку все объекты были заранее отнесены к известным нам классам, такой процесс построения дерева решений называется обучением с учителем (supervised learning). Процесс обучения также называют индуктивным обучением или индукцией деревьев (tree induction).
На сегодняшний день существует значительное число алгоритмов, реализующих деревья решений CART, C4.5, NewId, ITrule, CHAID, CN2 и т.д. Но наибольшее распространение и популярность получили следующие два:
- CART (Classification and Regression Tree) – это алгоритм построения бинарного дерева решений – дихотомической классификационной модели. Каждый узел дерева при разбиении имеет только двух потомков. Как видно из названия алгоритма, решает задачи классификации и регрессии.
- C4.5 – алгоритм построения дерева решений, количество потомков у узла не ограничено. Не умеет работать с непрерывным целевым полем, поэтому решает только задачи классификации.
Большинство из известных алгоритмов являются «жадными алгоритмами». Если один раз был выбран атрибут, и по нему было произведено разбиение на подмножества, то алгоритм не может вернуться назад и выбрать другой атрибут, который дал бы лучшее разбиение. И поэтому на этапе построения нельзя сказать даст ли выбранный атрибут, в конечном итоге, оптимальное разбиение.
Этапы построения деревьев решений
При построении деревьев решений особое внимание уделяется следующим вопросам: выбору критерия атрибута, по которому пойдет разбиение, остановки обучения и отсечения ветвей. Рассмотрим все эти вопросы по порядку.
Правило разбиения. Каким образом следует выбрать признак?
Для построения дерева на каждом внутреннем узле необходимо найти такое условие (проверку), которое бы разбивало множество, ассоциированное с этим узлом на подмножества. В качестве такой проверки должен быть выбран один из атрибутов. Общее правило для выбора атрибута можно сформулировать следующим образом: выбранный атрибут должен разбить множество так, чтобы получаемые в итоге подмножества состояли из объектов, принадлежащих к одному классу, или были максимально приближены к этому, т.е. количество объектов из других классов («примесей») в каждом из этих множеств было как можно меньше.
Были разработаны различные критерии, но мы рассмотрим только два из них:
Теоретико-информационный критерий
Алгоритм C4.5, усовершенствованная версия алгоритма ID3 (Iterative Dichotomizer), использует теоретико-информационный подход. Для выбора наиболее подходящего атрибута, предлагается следующий критерий:

|
(1) |
где, Info(T) – энтропия множества T, а

|
(2) |
Множества T1, T2, … Tn получены при разбиении исходного множества T по проверке X. Выбирается атрибут, дающий максимальное значение по критерию (1).
Впервые эта мера была предложена Р. Куинленом в разработанном им алгоритме ID3. Кроме вышеупомянутого алгоритма C4.5, есть еще целый класс алгоритмов, которые используют этот критерий выбора атрибута.
Статистический критерий
Алгоритм CART использует так называемый индекс Gini (в честь итальянского экономиста Corrado Gini), который оценивает «расстояние» между распределениями классов.
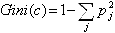
|
(3) |
Где c – текущий узел, а pj – вероятность класса j в узле c.
CART был предложен Л.Брейманом (L.Breiman) и др.
Правило остановки. Разбивать дальше узел или отметить его как лист?
В дополнение к основному методу построения деревьев решений были предложены следующие правила:
- Использование статистических методов для оценки целесообразности дальнейшего разбиения, так называемая «ранняя остановка» (prepruning). В конечном счете «ранняя остановка» процесса построения привлекательна в плане экономии времени обучения, но здесь уместно сделать одно важное предостережение: этот подход строит менее точные классификационные модели и поэтому ранняя остановка крайне нежелательна. Признанные авторитеты в этой области Л.Брейман и Р. Куинлен советуют буквально следующее: «Вместо остановки используйте отсечение».
- Ограничить глубину дерева. Остановить дальнейшее построение, если разбиение ведет к дереву с глубиной превышающей заданное значение.
- Разбиение должно быть нетривиальным, т.е. получившиеся в результате узлы должны содержать не менее заданного количества примеров.
Этот список эвристических правил можно продолжить, но на сегодняшний день не существует такого, которое бы имело большую практическую ценность. К этому вопросу следует подходить осторожно, так как многие из них применимы в каких-то частных случаях.
Правило отсечения. Каким образом ветви дерева должны отсекаться?
Очень часто алгоритмы построения деревьев решений дают сложные деревья, которые «переполнены данными», имеют много узлов и ветвей. Такие «ветвистые» деревья очень трудно понять. К тому же ветвистое дерево, имеющее много узлов, разбивает обучающее множество на все большее количество подмножеств, состоящих из все меньшего количества объектов.
Ценность правила, справедливого скажем для 2-3 объектов, крайне низка, и в целях анализа данных такое правило практически непригодно. Гораздо предпочтительнее иметь дерево, состоящее из малого количества узлов, которым бы соответствовало большое количество объектов из обучающей выборки.
И тут возникает вопрос: а не построить ли все возможные варианты деревьев, соответствующие обучающему множеству, и из них выбрать дерево с наименьшей глубиной? К сожалению, это задача является NP-полной, это было показано Л. Хайфилем (L. Hyafill) и Р. Ривестом (R. Rivest), и, как известно, этот класс задач не имеет эффективных методов решения.
Для решения вышеописанной проблемы часто применяется так называемое отсечение ветвей (pruning).
Пусть под точностью (распознавания) дерева решений понимается отношение правильно классифицированных объектов при обучении к общему количеству объектов из обучающего множества, а под ошибкой – количество неправильно классифицированных. Предположим, что нам известен способ оценки ошибки дерева, ветвей и листьев. Тогда, возможно использовать следующее простое правило:
- построить дерево;
- отсечь или заменить поддеревом те ветви, которые не приведут к возрастанию ошибки.
В отличии от процесса построения, отсечение ветвей происходит снизу вверх, двигаясь с листьев дерева, отмечая узлы как листья, либо заменяя их поддеревом.
Хотя отсечение не является панацеей, но в большинстве практических задач дает хорошие результаты, что позволяет говорить о правомерности использования подобной методики.

Правила
Иногда даже усеченные деревья могут быть все еще сложны для восприятия. В таком случае, можно прибегнуть к методике извлечения правил из дерева с последующим созданием наборов правил, описывающих классы.
Для извлечения правил необходимо исследовать все пути от корня до каждого листа дерева. Каждый такой путь даст правило, где условиями будут являться проверки из узлов встретившихся на пути.
Преимущества использования деревьев решений
Рассмотрев основные проблемы, возникающие при построении деревьев, было бы несправедливо не упомянуть об их достоинствах:
- быстрый процесс обучения;
- генерация правил в областях, где эксперту трудно формализовать свои знания;
- извлечение правил на естественном языке;
- интуитивно понятная классификационная модель;
- высокая точность прогноза, сопоставимая с другими методами (статистика, нейронные сети);
- построение непараметрических моделей.
В силу этих и многих других причин, методология деревьев решений является важным инструментом в работе каждого специалиста, занимающегося анализом данных, вне зависимости от того практик он или теоретик.
Области применения деревьев решений
Деревья решений являются прекрасным инструментом в системах поддержки принятия решений, интеллектуального анализа данных (data mining).
В состав многих пакетов, предназначенных для интеллектуального анализа данных, уже включены методы построения деревьев решений. В областях, где высока цена ошибки, они послужат отличным подспорьем аналитика или руководителя
Деревья решений успешно применяются для решения практических задач в следующих областях:
- Банковское дело. Оценка кредитоспособности клиентов банка при выдаче кредитов.
- Промышленность. Контроль за качеством продукции (выявление дефектов), испытания без разрушений (например проверка качества сварки) и т.д.
- Медицина. Диагностика различных заболеваний.
- Молекулярная биология. Анализ строения аминокислот.
Это далеко не полный список областей где можно использовать деревья решений. Не исследованы еще многие потенциальные области применения.
Список литературы:
- J. Ross Quinlan. C4.5: Programs for Machine learning. Morgan Kaufmann Publishers 1993
- S.Murthy. Automatic construction of decision trees from data: A Multi-disciplinary survey 1997
- W. Buntine. A theory of classification rules. 1992
- Machine Learning, Neural and Statistical Classification. Editors D. Mitchie et.al. 1994
- К. Шеннон. Работы по теории информации и кибернетике. М. Иностранная литература, 1963
- С.А. Айвазян, В.С Мхитарян Прикладная статистика и основы эконометрики, М. Юнити, 1998
|
 материалы
материалы  справочник
справочник  форум
форум  гостевая
гостевая  ссылки
ссылки