Имеется следующая задача – на двумерной карте с
препятствиями проложить путь из точки А в точку Б. Карта задана
в виде двумерного массива с двумя типами клеток – проходимыми и
непроходимыми.
Пусть у нас есть участок карты, через который необходимо
пройти (рис 1).
 |
Рис. 1. |
Для обхода препятствия воспользуемся широко известным
алгоритмом выхода из лабиринта, а именно – держась одной рукой
за стену и двигаясь вдоль нее, мы рано или поздно придем к
выходу любого лабиринта при условии, что мы стартовали из его
входа. Если же за начало взята любая стена внутри лабиринта, то
возможна ситуация когда процесс зациклится (например, вокруг
колонны).
Однако в данной задаче все довольно просто – на карте есть
непрерывная область непроходимых клеток (их будем именовать
«стенами»), которая пересекается с прямой, соединяющей точки А –
начало пути и Б – конец пути. Необходимо обойти это препятствие.
Надо заметить, что в качестве «непрерывности» можно использовать
самое строгое условие связности, а именно: две клетки считаются
соседними, если хотя бы одна пара соответсвующих координат
отличается на 1. То есть, две клетки по диагонали будут
считаться одной областью.
Для начала введем несколько переменных.
- Пусть P(x_p, y_p) – точка пути, непосредственно прилегающей
к препятствию. То есть, следующая за ней точка будет уже
принадлежать препятствию (см. рис 1).
- Пусть W(x_w, y_w) – точка пути, лежащей непосредственно
после точки P, то есть – это первая точка, принадлежащая
препятствию и линии пути (см. рис 1).
Необходимо попасть из точки P в точку D. Следует заметить,
что точка P находится там где она нарисована только в начале
пути, по мере движения она будет перемещаться по направлению к
точке D.
В условии алгоритма говорится о том, что надо держаться
одной рукой за стену, иными словами, всегда с одной и той же (!)
стороны от нас должна находиться стена. Как этого достичь на
дискретном поле? Рассмотрим этакие «диполи» на рис 2.
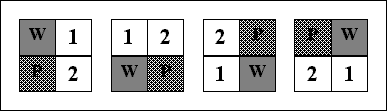 |
Рис. 2. |
Как и прежде, буквой P тут обозначены клетки пути, а буквой
W – клетки стены. Кроме того, цифрой «1» обозначены клетки,
стоящие справа от клетки стены, а цифрой «2» – клетки, стоящие
справа от клетки пути. Как можно говорить о направлениях в
данном случае? Направление задается двумя точками, которые можно
рассматривать как координаты вектора – начало вектора в точке P,
конец – в точке W.
Итак, для того, чтобы иметь возможность двигаться вдоль
стены надо иметь возможность однозначно определять координаты
точек «1» и «2». То есть, по сути, мы имеем дело с обходом
препятствия с помощью левой руки.
Формулы для координат соответсвующих точек представлены
ниже.
- x1 = x_w – (y_w - y_p); x2 = x_p – (y_w - y_p);
- y1 = y_w – (x_p - x_w); y2 = y_p – (x_p - x_w);
Если для примера подставить в эти формулы значения, то можно
убедиться, что они дают верные координаты для всех случаев.
Однако встает вопрос – каким образом обрабатывать клетки,
стоящие по диагонали? Тут возможны два случая – когда
диагонально стоящие клетки получаются при пересечении линии пути
с препятствием (как на рисунке 1) и когда они встречаются в ходе
выполнения алгоритма, например, при обходе угловых точек. В
первом случае все просто – надо выбирать точки P и W так, чтобы
они были 4-х связными соседями, то есть не стояли бы по
диагонали. Второй случай поясним из алгоритма работы всего
механизма перемещения.
Ищем вокруг текущей точки пути (там, где мы стоим,
фактически), клетку стены, за которую бы «ухватиться» рукой для
дальнейшего движения, то есть, если точка «2» непроходима, то W
= «2», выход. Если «2» проходима, то .проверяем точку «1», если
и она проходима, то P = «1», выход. Если «1» непроходима, то W =
«1», P = «2», выход.
Таким образом, мы как-бы перескакиваем через диагональные
клетки для пути, и вовсе не рассматриваем таковые для стен, если
есть рядом стоящие «не диагональные» непроходимые клетки.
Уяснить все это можно для себя, взяв карандаш и бумагу и
просмотрев все варианты «вручную».
Каким образом можно определить конец работы алгоритма? Все
зависит от конкретной реализации. Можно как-то помечать клетки
карты, проводя по ним линию пути, а наткнувшись на таковую при
обходе, прекратить работу. Важно следить за тем, чтобы это была
действительно точка D, а не какя-то другая, находящаяся между А
и P. Сделать это можно, пронумеровав все точки пути и
отбрасывать те из них, номер которых меньше чем номер стартовой
точки P.
Фролов Андрей. 12.06.2000
P.S. Алгоритм был получен в результате работы над проектом StarCrusade.
P.P.S. Исходный код из игры, который демонстрирует работу алгоритма -
 (1.16 Кб) (1.16 Кб)
|
 материалы
материалы  справочник
справочник  форум
форум  гостевая
гостевая  ссылки
ссылки