Введение в Генетические Алгоритмы

Генетические алгоритмы (ГА) - это стохастические, эвристические оптимизационные методы, впервые предложенные Холландом (1975). Они основываются на идее эволюции с помощью естественного отбора, выдвинутой Дарвином (1857).

1. Введение в генетические алгоритмы

ГА работают с совокупностью "особей" - популяцией, каждая из которых представляет возможное решение данной проблемы. Каждая особь оценивается мерой ее "приспособленности" согласно тому, насколько "хорошо" соответствующее ей решение задачи. В природе это эквивалентно оценке того, насколько эффективен организм при конкуренции за ресурсы. Наиболее приспособленные особи получают возможность "воспроизводить" потомство с помощью "перекрестного скрещивания" с другими особями популяции. Это приводит к появлению новых особей, которые сочетают в себе некоторые характеристики, наследуемые ими от родителей. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков, так что те свойства, которыми они обладали, будут постепенно исчезать из популяции в процессе эволюции. Иногда происходят мутации, или спонтанные изменения в генах.

Таким образом, из поколения в поколение, хорошие характеристики распространяются по всей популяции. Скрещивание наиболее приспособленных особей приводит к тому, что исследуются наиболее перспективные участки пространства поиска. В конечном итоге популяция будет сходиться к оптимальному решению задачи. Преимущество ГА состоит в том, что он находит приблизительные оптимальные решения за относительно короткое время.

ГА состоит из следующих компонент:

• Хромосома. Решение рассматриваемой проблемы. Состоит из генов.
• Начальная популяция хромосом.
• Набор операторов для генерации новых решений из предыдущей популяции.
• Целевая функция для оценки приспособленности (fitness) решений.

Чтобы применять ГА к задаче, сначала выбирается метод кодирование решений в виде строки. Фиксированная длина (l-бит) двоичной кодировки означает, что любая из 2^l возможных бинарных строк представляет возможное решение задачи.

По существу, такая кодировка соответствует разбиению пространства параметров на гиперкубы, которым соответствуют уникальные комбинации битов в строке - хромосоме. Для установления соответствия между гиперкубами разбиения области и бинарными строками, описывающими номера таких гиперкубов, кроме обычной двоичной кодировки использовался рефлексивный код Грея. Код Грея предпочтительнее обычного двоичного тем, что обладает свойством непрерывности бинарной комбинации: изменение кодируемого числа на единицу соответствует изменению кодовой комбинации только в одном разряде.

Кодирование в двоичный код и код Грея может быть продемонстрировано с помощью следующего примера.

2. Операторы ГА

Стандартные операторы для всех типов генетических алгоритмов это: селекция, скрещивание и мутация.

2.1 Селекция

Оператор селекции (reproduction, selection) осуществляет отбор хромосом в соответствии со значениями их функции приспособленности. Существуют как минимум два популярных типа оператора селекции: рулетка и турнир.

• Метод рулетки (roulette-wheel selection) - отбирает особей с помощью n "запусков" рулетки. Колесо рулетки содержит по одному сектору для каждого члена популяции. Размер i-ого сектора пропорционален соответствующей величине P_sel(i) вычисляемой по формуле:
  
  При таком отборе члены популяции с более высокой приспособленностью с большей вероятностью будут чаще выбираться, чем особи с низкой приспособленностью.
  
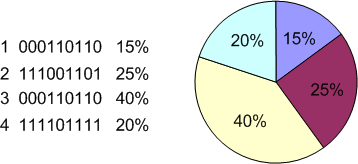
  Рис. 1. Оператор селекции типа колеса рулетки
  с пропорциональными функции приспособленности секторами

• Турнирный отбор (tournament selection) реализует n турниров, чтобы выбрать n особей. Каждый турнир построен на выборке k элементов из популяции, и выбора лучшей особи среди них. Наиболее распространен турнирный отбор с k=2.

2.2. Скрещивание

Оператор скрещивание (crossover) осуществляет обмен частями хромосом между двумя (может быть и больше) хромосомами в популяции. Может быть одноточечным или многоточечным. Одноточечный кроссовер работает следующим образом. Сначала, случайным образом выбирается одна из l-1 точек разрыва. Точка разрыва - участок между соседними битами в строке. Обе родительские структуры разрываются на два сегмента по этой точке. Затем, соответствующие сегменты различных родителей склеиваются и получаются два генотипа потомков.

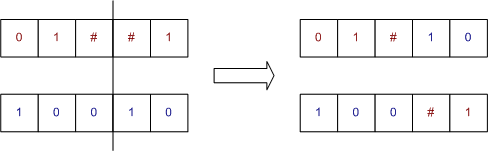
Рис. 2. Одноточечный оператор скрещивания (точка разрыва равна трем)

2.3. Мутация

Мутация (mutation) - стохастическое изменение части хромосом. Каждый ген строки, которая подвергается мутации, с вероятностью P_mut (обычно очень маленькой) меняется на другой ген.

Рис. 3. Оператор мутации (четвертый ген мутировал)

3. Алгоритм работы ГА

Работа ГА представляет собой итерационный процесс, который продолжается до тех пор, пока не выполнятся заданное число поколений или какой-либо иной критерий останова. На каждом поколении ГА реализуется отбор пропорционально приспособленности, кроссовер и мутация.

Алгоритм работы простого ГА выглядит следующим образом:

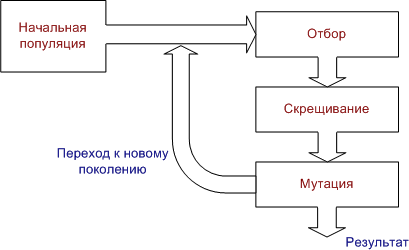
Рис. 4. Алгоритм работы классического ГА

  НАЧАЛО /* генетический алгоритм */
      Создать начальную популяцию
      Оценить приспособленность каждой особи
      останов = FALSE
      ПОКА НЕ останов ВЫПОЛНЯТЬ
      НАЧАЛО /* создать популяцию нового поколения */ 
          ПОВТОРИТЬ (размер_популяции/2) РАЗ
          НАЧАЛО /* цикл воспроизводства */ 
              Выбрать две особи с высокой приспособленностью из предыдущего поколения
              Скрестить выбранные особи и получить двух потомков 
              Оценить приспособленности потомков 
              Поместить потомков в новое поколение 
          КОНЕЦ
          ЕСЛИ популяция сошлась, ТО останов = TRUE 
      КОНЕЦ
  КОНЕЦ