|
В этой главе излагается материал,
значение которого для вычислительной математики и всего того, что по-английски
именуют «computer sciences», выходит далеко за
пределы нейроинформатики. Со временем он безусловно будет включен в программы
университетских курсов математического анализа.
Обсудим одну "очевидную"
догму, без разрушения которой было бы невозможно эффективное обучение нейронных
сетей. Пусть вычислительные затраты (оцениваемые временем, затраченным
некоторым универсальным вычислительным устройством) на вычисление одного
значения функции n переменных H(x1,...,xn)
примерно равны T . Сколько времени
потребуется тому же устройству на вычисление gradH (при разумном составлении программы)?
Большинство математиков с университетским дипломом ответит:
Это неверно! Правильный ответ:
где C - константа, не зависящая от размерности
n (в большинстве случаев C~3).
Для всех функций многих переменных,
встречающихся на практике, необходимые вычислительные затраты на поиск их
градиента всего лишь в два-три раза превосходят затраты на вычисление одного
значения функции. Это удивительно ‑ ведь координатами вектора градиента
служат n частных производных, а затраты на
вычисление одной такой производной в общем случае примерно такие же, как и на
вычисление значения функции. Почему же вычисление всех их вместе дешевле, чем
по-отдельности?
«Чудо» объясняется довольно просто:
нужно рационально организовать вычисление производных сложной функции многих
переменных, избегая дублирования. Для этого необходимо подробно представить
само вычисление функции, чтобы потом иметь дело не с «черным ящиком»,
преобразующим вектор аргументов в значение функции, а с детально описанным
графом вычислений.
Поиск gradH удобно представить как некоторый двойственный процесс над
структурой вычисления H.
Промежуточные результаты, появляющиеся при вычислении градиента, являются ни
чем иным, как множителями Лагранжа. Оказывается, что если представить H как сложную функцию, являющуюся
суперпозицией функций малого числа переменных (а по-другому вычислять функции
многих переменных мы не умеем), и аккуратно воспользоваться правилом
дифференцирования сложной функции, не производя по дороге лишних вычислений и
сохраняя полезные промежуточные результаты, то вычисление всей совокупности ¶H/¶xi (i =1,...,n)
немногим сложнее, чем одной из этих функций ‑ они все собраны из
одинаковых блоков.
Я не знаю, кто все это придумал
первым. В нейроинформатике споры о приоритете ведутся до сих пор. Конец
переоткрытиям положили две работы 1986 г.: Румельхарта, Хинтона и Вильямса
[1,2] и Барцева и Охонина [3]. Однако первые публикации относятся к 70-м и даже
60-м годам нашего столетия. По мнению В.А.Охонина, Лагранж и Лежандр также
вправе претендовать на авторство метода.
1. Обучение нейронных сетей как минимизация функции ошибки
Построение обучения как оптимизации
дает нам универсальный метод создания нейронных сетей для решения задач. Если
сформулировать требования к нейронной сети, как задачу минимизации некоторой
функции - оценки, зависящей от части сигналов (входных, выходных, ...) и от
параметров сети, то обучение можно рассматривать как оптимизацию и строить
соответствующие алгоритмы, программное обеспечение и, наконец, устройства
(hardware). Функция оценки обычно довольно просто (явно) зависит от части
сигналов - входных и выходных. Ее зависимость от настраиваемых параметров сети
может быть сложнее и включать как явные компоненты (слагаемые,
сомножители,...), так и неявные - через сигналы (сигналы, очевидно, зависят от
параметров, а функция оценки - от сигналов).
За пределами задач, в которых
нейронные сети формируются по явным правилам (сети Хопфилда, проективные сети,
минимизация аналитически заданных функций и т.п.) нам неизвестны случаи, когда
требования к нейронной сети нельзя было бы представить в форме минимизации
функции оценки. Не следует путать такую постановку задачи и ее весьма частный
случай - "обучение с учителем". Уже метод динамических ядер,
описанный в предыдущей главе, показывает, каким образом обучение без учителя в
задачах классификации может быть описано как минимизация целевой функции,
оценивающей качество разбиения на классы.
Если для решения задачи не удается
явным образом сформировать сеть, то проблему обучения можно, как правило,
сформулировать как задачу минимизации оценки. Осторожность предыдущей фразы
("как правило") связана с тем, что на самом деле нам неизвестны и никогда
не будут известны все возможные задачи для нейронных сетей, и, быть может,
где-то в неизвестности есть задачи, которые несводимы к минимизации оценки.
Минимизация оценки - сложная
проблема: параметров астрономически много (для стандартных примеров, реализуемых
на РС - от 100 до 1000000), адаптивный рельеф (график оценки как функции от
подстраиваемых параметров) сложен, может содержать много локальных минимумов,
извилистых оврагов и т.п.
Наконец, даже для того, чтобы
воспользоваться простейшими методами гладкой оптимизации, нужно вычислять
градиент функции оценки. Здесь мы сталкиваемся с одной "очевидной"
догмой, без разрушения которой было бы невозможно эффективное обучение
нейронных сетей.
2. Граф вычисления сложной функции
Сложная функция задается с помощью
суперпозиции некоторого набора «простых». Простые функции принадлежат исходно
задаваемому конечному множеству F. Формально они выделены
только принадлежностью к множеству F - никаких обязательных
иных отличий этих функций от всех прочих в общем случае не предполагается.
В этом разделе мы изучим способы
задания сложных функций, то есть формулы и соответствующие им графы. Свойства
самих функций нас сейчас не интересуют (будем рассматривать ноты, а не слушать
музыку).
Теория выражений, определяющих сложные
функции, является простейшим разделом математической логики, в которой сами эти
выражения называются термами [4].
Термы - это правильно построенные
выражения в некотором формальном языке. Чтобы задать такой язык, необходимо
определить его алфавит. Он состоит из
трех множеств символов:
- C - множество символов, обозначающих константы;
- V - множество символов, обозначающих переменные;
- F - множество функциональных символов,
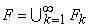 , где , где
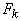 - множество символов для обозначения функций k переменных.
- множество символов для обозначения функций k переменных.
Вводя различные множества символов,
мы постоянно обращаемся к их
интерпретации («... символы, обозначающие...»). Строго говоря, это не нужно
- можно (а с чисто формальной точки зрения - и должно) описать все правила
действия с символами, не прибегая к их интерпретации, однако ее использование
позволяет сократить изложение формальных правил за счет обращения к имеющемуся
содержательному опыту.
Термы определяются индуктивно:
- любой символ из
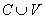 есть терм; есть терм;
- если
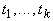 - термы и
- термы и 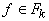 ,
то ,
то 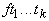 - терм.
- терм.
Множество термов T представляет собой объединение:
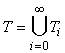 , ,
где 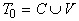 , ,
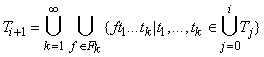 (
(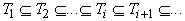 ). ).
Удобно разбить T на
непересекающиеся множества - слои 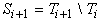 (
(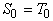 ). Элементы ). Элементы 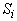 будем называть
термами глубины i или i-слойными
термами. Множеству
будем называть
термами глубины i или i-слойными
термами. Множеству 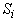 принадлежат
выражения, обозначающие те функции от термов предыдущих слоев
принадлежат
выражения, обозначающие те функции от термов предыдущих слоев
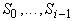 , которые сами им не
принадлежат 2. , которые сами им не
принадлежат 2.
Для оперирования с термами очень
полезны две теоремы [4].
Теорема 1 (о построении термов).
Каждый терм t единственным
образом представляется в виде 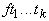 , где f - первый символ в t, , где f - первый символ в t, 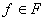 , число k определяется по f ( , число k определяется по f (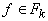 ), а ), а 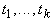 - термы.
- термы.
Эта теорема является точной
формулировкой эквивалентности используемой бесскобочной и обычной записи.
Пусть u и v - выражения, то есть
последовательности символов алфавита. Скажем, что u входит в v, если существуют такие
выражения p и q (возможно,
пустые), что v совпадает с puq.
Теорема 2 (о вхождении терма в
терм). Пусть 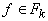 , , 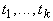 - термы, t представляется в виде
- термы, t представляется в виде 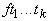 , t - терм
и t входит в t. Тогда или t
совпадает с t, или t
входит в одно из , t - терм
и t входит в t. Тогда или t
совпадает с t, или t
входит в одно из 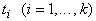 . .
Доказываются эти теоремы
элементарной индукцией по длине термов [4]. В доказательстве теоремы 2
выделяется лемма, представляющая и самостоятельный интерес.
Лемма 1. Каждое вхождение любого
символа в терм t начинает вхождение
некоторого терма в t.
Определим отношение между термами 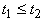 индуктивным образом
«сверху вниз» - по глубине вхождения:
индуктивным образом
«сверху вниз» - по глубине вхождения:
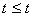 ;
;
- если t совпадает с
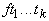 , , 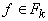 и
и 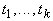 - термы, то
- термы, то 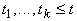 ;
;
- если
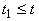 и
и 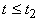 , то , то 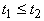 . .
Согласно теореме 2, 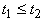 тогда и только тогда,
когда
тогда и только тогда,
когда 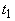 входит в
входит в 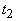 . .
Для каждого терма t определим множество входящих в него термов 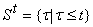 . Если . Если 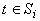 , то при , то при 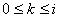 непусты множества
непусты множества 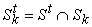 . При этом множество . При этом множество 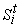 состоит из одного элемента - исходного терма t.
состоит из одного элемента - исходного терма t.
Свяжем с термом t ориентированный граф 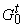 с вершинами,
взаимнооднозначно соответствующими термам из
с вершинами,
взаимнооднозначно соответствующими термам из 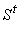 . Будем одинаково обозначать вершины и соответствующие им
термы. Пара вершин . Будем одинаково обозначать вершины и соответствующие им
термы. Пара вершин 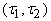 образует
ориентированное от
образует
ориентированное от 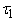 к
к 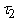 ребро графа
ребро графа 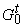 , если терм , если терм 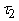 имеет вид
имеет вид 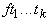 , , 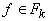 , , 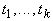 - термы и один из них
- термы и один из них
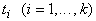 совпадает с
совпадает с 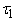 . Вершины графа . Вершины графа 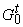 удобно располагать по
слоям
удобно располагать по
слоям 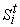 . .
Для произвольного графа G будем обозначать v(G) множество вершин, а e(G) -
множество ребер G.
Возьмем для примера выражение для
сложной функции
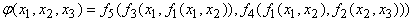 . . |
(3) |
В принятой выше бесскобочной префиксной
записи оно имеет вид
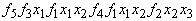 , , |
(3¢) |
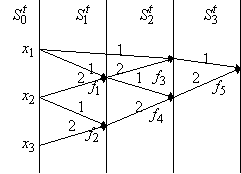
Рис. 1. Пример графа  . Около вершин и над ребрами указаны соответствующие метки . Около вершин и над ребрами указаны соответствующие метки
|
где все
функциональные символы принадлежат 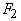 . .
Граф 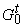 для этого терма
изображен на рис. 1.
для этого терма
изображен на рис. 1.
Для того, чтобы терм однозначно
восстанавливался по графу, необходимы еще два дополнения.
1.
) метку p(t)
- символ алфавита. Если вершина принадлежит нулевому слою 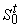 , то ей соответствует терм, совпадающий с символом из , то ей соответствует терм, совпадающий с символом из 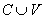 . Этот символ и сопоставляется вершине в качестве метки. Если
вершина принадлежит . Этот символ и сопоставляется вершине в качестве метки. Если
вершина принадлежит 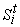 (i>0), то
меткой служит функциональный символ: вершине t
сопоставляется
(i>0), то
меткой служит функциональный символ: вершине t
сопоставляется 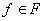 , если t
имеет вид , если t
имеет вид 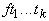 , где , где 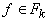 , а , а 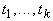 - термы.
- термы.
2.
), приходящему в вершину t,
сопоставим метку P(t¢,t) - конечное множество натуральных чисел (номеров):
пусть терм t имеет вид 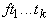 , где , где 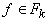 , а , а 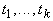 - термы, тогда ребру
(t¢,t) сопоставляется множество тех i (1£i£k), для которых
t¢
совпадает с
- термы, тогда ребру
(t¢,t) сопоставляется множество тех i (1£i£k), для которых
t¢
совпадает с 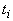 . На практике в большинстве случаев эта метка состоит из
одного номера, но возможны и другие варианты - так же, как функции вида f(x,x). Для
графических иллюстраций удобно ребра (t¢,t), имеющие в своей метке P(t¢,t)
больше одного номера, рисовать как пучок ребер, идущих от вершины t¢ к вершине t
- по одному такому ребру для каждого номера из P(t¢,t);
этот номер и будет меткой соответствующего ребра из пучка. . На практике в большинстве случаев эта метка состоит из
одного номера, но возможны и другие варианты - так же, как функции вида f(x,x). Для
графических иллюстраций удобно ребра (t¢,t), имеющие в своей метке P(t¢,t)
больше одного номера, рисовать как пучок ребер, идущих от вершины t¢ к вершине t
- по одному такому ребру для каждого номера из P(t¢,t);
этот номер и будет меткой соответствующего ребра из пучка.
Граф 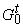 вместе со всеми
метками будем обозначать
вместе со всеми
метками будем обозначать 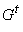 . На рис. 1 указаны соответствующие метки для разобранного
примера. . На рис. 1 указаны соответствующие метки для разобранного
примера.
Итак, для всякого терма t построен ориентированный граф 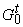 и две функции: первая
сопоставляет каждой вершине tÎv(
и две функции: первая
сопоставляет каждой вершине tÎv(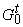 ) символ алфавита ) символ алфавита 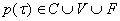 , вторая (обозначим ее P) -
каждому ребру (t¢,t)Îe(
, вторая (обозначим ее P) -
каждому ребру (t¢,t)Îe(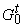 ) - конечное множество натуральных чисел P(t¢,t).
Отмеченный граф - набор ( ) - конечное множество натуральных чисел P(t¢,t).
Отмеченный граф - набор (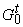 ,p,P)
обозначаем ,p,P)
обозначаем 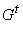 . Функции p и P
удовлетворяют следующему ограничению: . Функции p и P
удовлетворяют следующему ограничению:
А) если для данного 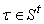 множество входящих
ребер (t¢,t) непусто, то
множество входящих
ребер (t¢,t) непусто, то 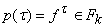 (является k-местным функциональным символом при некотором k) и семейство множеств
(является k-местным функциональным символом при некотором k) и семейство множеств
{P(t¢,t)|(t¢,t)Îe(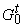 ) } ) }
при фиксированном t образует разбиение множества номеров {1,...,k}, то есть
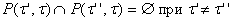 , ,
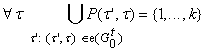 . .
На этом завершается изложение
основных формальных конструкций. Прежде, чем переходить к интерпретации,
сформулируем теорему об эквивалентности графического и формульного
представления термов.
Пусть G -
конечный ориентированный граф, не имеющий ориентированных циклов, и в G существует и единственна такая вершина 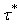 , к которой от любой вершины ведет ориентированный путь.
Пусть, далее, заданы две функции: p -
на множестве вершин G со
значениями в множестве символов алфавита и P - на множестве ребер G со значениями в множестве конечных наборов натуральных
чисел и выполнено условие А. , к которой от любой вершины ведет ориентированный путь.
Пусть, далее, заданы две функции: p -
на множестве вершин G со
значениями в множестве символов алфавита и P - на множестве ребер G со значениями в множестве конечных наборов натуральных
чисел и выполнено условие А.
Теорема 3. Существует и единственен
терм t, для которого 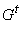 =(G,p,P).
=(G,p,P).
Доказательство
проводится в два этапа. Сначала в G устанавливается
послойная структура: строится разбиение множества вершин G: 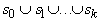 . Множество . Множество 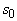 состоит из тех
вершин, к которым не ведет ни одного ребра - из-за отсутствия ориентированных
циклов такие вершины существуют. Множество
состоит из тех
вершин, к которым не ведет ни одного ребра - из-за отсутствия ориентированных
циклов такие вершины существуют. Множество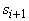 состоит из тех вершин, к которым ведут ребра только из
элементов
состоит из тех вершин, к которым ведут ребра только из
элементов 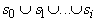 . Последний непустой элемент в последовательности . Последний непустой элемент в последовательности 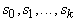 состоит из одной
вершины
состоит из одной
вершины 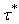 , все предшествующие элементы этой последовательности
непусты, а объединение всех , все предшествующие элементы этой последовательности
непусты, а объединение всех 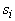 содержит все вершины G.
содержит все вершины G.
Доказательство основного
утверждения теоремы проводится индукцией по числу слоев k.
Интерпретация
сопоставляет терму сложную функцию. Она строится так. Задается некоторое
множество D - область интерпретации. Каждой
константе с, входящей в
интерпретируемый терм t, сопоставляется элемент из D (cÎD), каждому
k-местному функциональному символу f,
входящему в t, сопоставляется функция k переменных 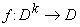 (мы сохраняем
одинаковое обозначение для символов и их интерпретации, это вполне
соответствует интуиции и не должно приводить к путанице). Каждой переменной,
входящей в интерпретируемый терм t, сопоставляется
переменная, пробегающая D. В результате терму t сопоставляется функция n переменных
(мы сохраняем
одинаковое обозначение для символов и их интерпретации, это вполне
соответствует интуиции и не должно приводить к путанице). Каждой переменной,
входящей в интерпретируемый терм t, сопоставляется
переменная, пробегающая D. В результате терму t сопоставляется функция n переменных 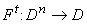 , где n - число различных
символов переменных, входящих в t. Эта «сложная» функция
получается суперпозицией «простых» функций, соответствующих функциональным
символам.
, где n - число различных
символов переменных, входящих в t. Эта «сложная» функция
получается суперпозицией «простых» функций, соответствующих функциональным
символам.
Если 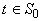 , то есть терм является константой или переменной, то вместо
сложной функции , то есть терм является константой или переменной, то вместо
сложной функции 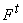 получаем
константу или тождественную функцию id, переводящую значение переменной в него же. Если
получаем
константу или тождественную функцию id, переводящую значение переменной в него же. Если 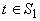 , то соответствующая функция является «простой». Истинные
сложные функции появляются, начиная со слоя , то соответствующая функция является «простой». Истинные
сложные функции появляются, начиная со слоя 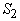 . .
Заметим, что заданная интерпретация
терма t одновременно определяет интерпретацию каждого терма,
входящего в t.
Представим процесс вычисления
сложной функции 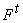 с помощью отмеченного
графа
с помощью отмеченного
графа 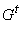 . Строится два представления: статическое (все результаты
промежуточных вычислений располагаются на графе) и динамическое (шаг за шагом,
слой за слоем). . Строится два представления: статическое (все результаты
промежуточных вычислений располагаются на графе) и динамическое (шаг за шагом,
слой за слоем).
Пусть задана интерпретация терма t и определены значения всех переменных, входящих в t. Тогда для любого терма t,
входящего в t, также задана интерпретация и
определены значения всех функций 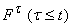 . Каждой вершине t, входящей в граф
. Каждой вершине t, входящей в граф 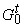 , сопоставляется значение функции , сопоставляется значение функции 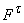 - элемент D. При этом вершинам нулевого слоя соответствуют значения
переменных и констант, а единственной вершине последнего (выходного) слоя -
значение
- элемент D. При этом вершинам нулевого слоя соответствуют значения
переменных и констант, а единственной вершине последнего (выходного) слоя -
значение 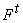 . Будем называть элементы D, соответствующие
вершинам, значениями этих вершин и
обозначать их Z(t). . Будем называть элементы D, соответствующие
вершинам, значениями этих вершин и
обозначать их Z(t).
Для каждой вершины t, принадлежащей ненулевому слою, можно выписать уравнение функционирования, связывающее
значения вершин. Пусть p(t)=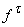 , , 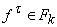 и in(t)
- совокупность входящих в t
ребер. Напомним, что совокупность меток ребер, оканчивающихся в t,
и in(t)
- совокупность входящих в t
ребер. Напомним, что совокупность меток ребер, оканчивающихся в t,
{P(t¢,t)|(t¢,t)Îin(t)}
образует разбиение
множества {1,2,...,k}.
Уравнение функционирования для
вершины t, принадлежащей
ненулевому слою, имеет вид
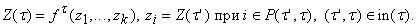 |
(4) |
В силу уравнения функционирования
(4), если для входящих в t
ребер (t¢,t)Îin(t) известны значения Z(t¢) и задана интерпретация символа p(t)=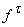 - метки вершины, то можно найти значение вершины Z(t).
На основании этого (очевидного) замечания строится динамическое представление
вычисления сложной функции.
- метки вершины, то можно найти значение вершины Z(t).
На основании этого (очевидного) замечания строится динамическое представление
вычисления сложной функции.
С каждой вершиной графа t , принадлежащей ненулевому слою, ассоциируется
автомат, вычисляющий функцию 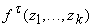 , где , где 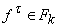 - метка вершины t. Автоматы срабатывают по слоям в дискретные моменты
времени (такты) - автоматы i-го слоя в i-й момент времени. В начальный момент сформированы значения
вершин нулевого слоя - известны значения переменных и констант. Они поступают
на входы автоматов первого слоя в соответствии с нумерацией аргументов. После i-го такта функционирования определены значения вершин,
принадлежащих слоям
- метка вершины t. Автоматы срабатывают по слоям в дискретные моменты
времени (такты) - автоматы i-го слоя в i-й момент времени. В начальный момент сформированы значения
вершин нулевого слоя - известны значения переменных и констант. Они поступают
на входы автоматов первого слоя в соответствии с нумерацией аргументов. После i-го такта функционирования определены значения вершин,
принадлежащих слоям 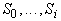 . На i+1-м такте автоматы i+1-го слоя вычисляют значения вершин i+1-го
слоя, получая входные сигналы с предыдущих слоев по правилу (4) - в
соответствии с метками входящих ребер. . На i+1-м такте автоматы i+1-го слоя вычисляют значения вершин i+1-го
слоя, получая входные сигналы с предыдущих слоев по правилу (4) - в
соответствии с метками входящих ребер.
3. Вычисления на ориентированном графе
Для дальнейшего полезно обобщение
изложенных конструкций, предназначенное для описания одновременного вычисления
нескольких сложных функций.
Пусть G - связный
(но не обязательно ориентированно связный) ориентированный граф без
ориентированных циклов. Как и выше, множество вершин G
обозначаем v(G), множество ребер - e(G). Пусть, далее, каждой вершине tÎv(G) сопоставлена метка - символ алфавита p(t), а каждому ребру (t¢,t)Îe(G) сопоставляется метка - конечное множество натуральных
чисел P(t¢,t) и выполнено условие согласования А: если для
данного tÎv(G)
множество входящих ребер (t¢,t) непусто, то 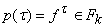 (является k-местным функциональным символом при некотором k) и семейство множеств {P(t¢,t)|(t¢,t)Îe(G)} при фиксированном t
образует разбиение множества номеров {1,...,k}.
(является k-местным функциональным символом при некотором k) и семейство множеств {P(t¢,t)|(t¢,t)Îe(G)} при фиксированном t
образует разбиение множества номеров {1,...,k}.
С помощью транзитивного замыкания G устанавливаем на множестве его вершин v(G) отношения частичного
порядка: t³t¢, если существует ориентированный путь, ведущий от t¢ к t.
Из-за отсутствия ориентированных циклов это отношение антисимметрично: если t³t¢
и t¢³t, то t
совпадает с t¢.
Минимальные вершины (к которым не ведет ни одного ребра) называем входными, а максимальные (от которых не
идет ни одного ребра) - выходными.
Обозначим множество входных вершин 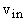 , а выходных - , а выходных - 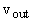 . Метки входных вершин являются символами переменных или
констант, метки остальных вершин - функциональные символы. . Метки входных вершин являются символами переменных или
констант, метки остальных вершин - функциональные символы.
Определим послойную структуру: v(G)= 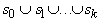 . Нулевой слой состоит из минимальных вершин, первый слой из
минимальных вершин графа, получаемого удалением из G нулевого
слоя и выходящих из него ребер и т.д. - i+1-й слой состоит из
минимальных вершин графа, получаемого удалением из G всех
вершин объединения . Нулевой слой состоит из минимальных вершин, первый слой из
минимальных вершин графа, получаемого удалением из G нулевого
слоя и выходящих из него ребер и т.д. - i+1-й слой состоит из
минимальных вершин графа, получаемого удалением из G всех
вершин объединения 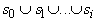 и содержащих их
ребер. Последний слой состоит только из выходных вершин. Предыдущие слои также
могут содержать выходные вершины.
и содержащих их
ребер. Последний слой состоит только из выходных вершин. Предыдущие слои также
могут содержать выходные вершины.
С каждой вершиной графа tÎv(G) однозначно связан терм (который мы, следуя традиции
предыдущего раздела, также будем обозначать t).
Для его построения удалим из G все вершины, кроме тех,
от которых к t можно пройти по
ориентированному пути, а также связанные с ними ребра. Полученный граф
обозначим 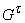 : v(
: v(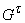 )={t¢Îv(G)|t³t¢}.
Граф
)={t¢Îv(G)|t³t¢}.
Граф 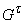 удовлетворяет
условиям теоремы 3, поэтому по нему единственным образом восстанавливается терм
(и соответствующая сложная функция).
удовлетворяет
условиям теоремы 3, поэтому по нему единственным образом восстанавливается терм
(и соответствующая сложная функция).
Пусть задано множество D - область интерпретации и указана интерпретация всех символов,
отмечающих вершины графа, а также значения переменных, отвечающих входным
вершинам. Тогда по уравнениям функционирования (4) (они полностью сохраняются и
для рассматриваемых графов) можно определить значения Z(t) для всех вершин графа. В результате определяются
значения всех сложных функций, формулы для которых являются термами,
соответствующими вершинам графа G.
Описанные общие графы могут
появляться в различных ситуациях. Для дальнейшего важно то, что такие графы
возникают, если из графа вычисления сложной функции удалить один или несколько
последних слоев.
4. Двойственное функционирование, дифференциальные операторы и градиент сложной функции
А. Производная сложной функции одного переменного
Основную идею двойственного
функционирования можно понять уже на простейшем примере. Рассмотрим вычисление
производной сложной функции одного переменного. Пусть заданы функции одного
переменного f1(A),
f2(A),... ,
fn(A) . Образуем из них сложную функцию
F(x)=fn (fn-1 (...(f1
(x))...)). (1)
Можно представить вычисление F(x)
как результат работы n автоматов,
каждый из которых имеет один вход и выдает на выходе значение fi (A), где A - входной сигнал (рис.2, а). Чтобы построить систему автоматов,
вычисляющую F¢(x), надо дополнить исходные автоматы такими, которые вычисляют
функции fi¢(A), где A - входной сигнал (важно различать производную fi по входному
сигналу, то есть по аргументу функции fi, и производную сложной функции fi(A(x)) по x; fi¢(A) ‑ производные по A).
Для вычисления F¢(x) потребуется еще цепочка из n-1 одинаковых автоматов, имеющих по два
входа, по одному выходу и подающих на выход произведение входов. Тогда формулу
производной сложной функции
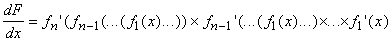
можно реализовать с помощью сети автоматов, изображенной на рис. 2, б. Сначала
по этой схеме вычисления идут слева направо: на входы f1 и f1'
подаются значения x, после вычислений
f1(x) это число подается на входы f2 и f2' и т.д. В конце цепочки оказываются вычисленными все fi (fi-1
(...)) и fi'(fi-1 (...)).
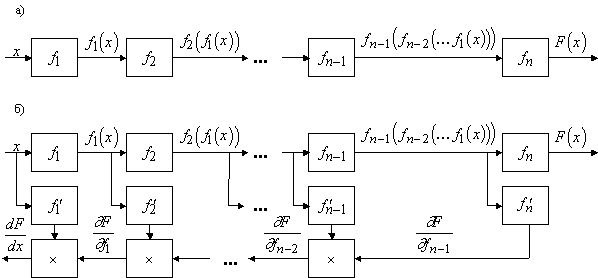
Рис. 2. Схематическое представление вычисления сложной
функции одного переменного и ее производных.
|
Тем самым, для каждого автомата
нижней строки, кроме самого правого, оказывается сформированным по одному
значению входа, а у самого правого - оба, поэтому он может сработать и начать
передачу сигнала в обратном направлении ‑ справа налево. Это обратное
движение есть последовательное вычисление попарных произведений и передача их
налево. В конце получаем dF/dx.
Б.
Двойственное функционирование и быстрое дифференцирование
Вычисление градиента сложной
функции многих переменных также будет представлено как некоторый вычислительный
процесс, в ходе которого сигналы перемещаются в обратном направлении - от
выходных элементов графа к входным. И так же, как при вычислении сложной
функции, будет явно представлено прохождение каждого узла (подобно тому, как
это сделано в уравнении функционирования (4)), а весь процесс в целом будет
складываться из таких элементарных фрагментов за счет структуры связей между
узлами. Сама эта структура - та же самая, что и для прямого процесса.
Всюду в этом разделе область
интерпретации - действительная прямая, а все функции дифференцируемы.
Основной инструмент при построении
двойственного функционирования - формула для дифференцирования «двухслойной»
сложной функции нескольких переменных
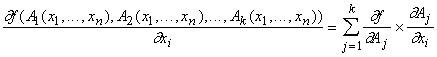 . . |
(5) |
При проведении индукции по числу
слоев нам придется использовать графы с несколькими выходными вершинами,
описанные в предыдущем разделе, поэтому сразу будем рассматривать этот более
общий случай.
Итак, пусть G - связный
(но не обязательно ориентированно связный) ориентированный граф без
ориентированных циклов. Как и выше, v(G) - множество вершин G, e(G) - множество ребер. Пусть, далее, каждой вершине tÎv(G) сопоставлена метка - символ алфавита p(t), а каждому ребру (t¢,t)Îe(G) сопоставляется метка - конечное множество натуральных
чисел P(t¢,t) и выполнено условие согласования А: если для
данного tÎv(G)
множество входящих ребер (t¢,t) непусто, то  (является k-местным функциональным символом при некотором k) и семейство множеств {P(t¢,t)|(t¢,t)Îe(G)} при фиксированном t
образует разбиение множества номеров {1,...,k}. Для каждой вершины tÎv(G) обозначим множество входящих в нее ребер in(t),
а выходящих из нее - out(t).
(является k-местным функциональным символом при некотором k) и семейство множеств {P(t¢,t)|(t¢,t)Îe(G)} при фиксированном t
образует разбиение множества номеров {1,...,k}. Для каждой вершины tÎv(G) обозначим множество входящих в нее ребер in(t),
а выходящих из нее - out(t).
Пусть указана интерпретация всех
символов, отмечающих вершины графа, значения переменных, отвечающих входным
вершинам и уравнениям функционирования (4) определены значения Z(t)
для всех вершин графа. В результате определены значения всех сложных функций,
формулы для которых являются термами, соответствующими вершинам графа G. Процесс вычисления Z(t)
будем называть прямым в противовес обратному или двойственному, к описанию которого мы переходим.
При заданных Z(t) для каждой вершины и каждого ребра строятся переменные двойственного функционирования (или,
более кратко, двойственные переменные).
Будем обозначать их m(t) для вершин и m(t¢,t)
- для ребер.
Для выходных вершин m(t)
являются независимыми переменными. Пусть их значения заданы. Для вершины t, не являющейся выходной, значение m(t)
есть сумма значений двойственных переменных, соответствующих выходящим из t ребрам:
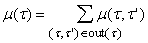 . . |
(6) |
Для ребра (t¢,t) значение m(t¢,t)
определяется согласно формуле (5):
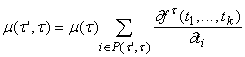 . . |
(7) |
В формуле (7) 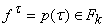 - метка ребра t,
- метка ребра t, 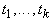 - аргументы «простой»
функции
- аргументы «простой»
функции 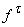 , а производные , а производные 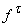 берутся при условиях,
определяемых прямым процессом:
берутся при условиях,
определяемых прямым процессом:
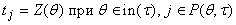 . . |
(8) |
Для каждого jÎ{1,...,k} такое q существует и единственно в силу того, что метки
входящих в вершину t
ребер образуют разбиение множества номеров {1,...,k}.
В самом распространенном случае все
метки ребер P(t¢,t) содержат по одному элементу. В этом случае формула
(7) приобретает особенно простой вид
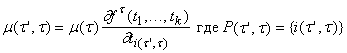 . (7¢) . (7¢)
Используя (6)-(8), можно записать
правила вычисления двойственных переменных для вершин, не использующие
двойственных переменных для ребер:
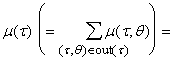
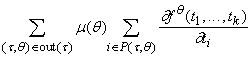 , , |
(9) |
где производные 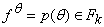 берутся при условиях
берутся при условиях
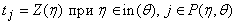 . . |
(10) |
Греческими
буквами t, q,
h здесь обозначены
вершины графа.
Опять же, в распространенном
случае, когда все P(t¢,t) одноэлементны, применяем (7¢) вместо (7) и
получаем
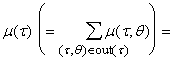
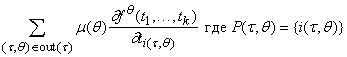 (9¢)
(9¢)
Напомним, что каждой вершине t, принадлежащей ненулевому слою графа G, соответствуют терм t
и сложная функция 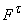 от независимых
переменных и констант, отмечающих вершины нулевого слоя G.
от независимых
переменных и констант, отмечающих вершины нулевого слоя G.
Процесс вычисления двойственных
переменных организуется послойно от выходных вершин к входным и часто
называется процессом обратного
распространения (back propagation)
или просто обратным процессом.
Теорема 5. Пусть задана интерпретация
всех символов, отмечающих вершины графа G, определены значения
независимых переменных (а также констант), соответствующих вершинам входного
слоя 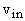 и значения
независимых переменных двойственного функционирования m(t) для вершин выходного слоя
и значения
независимых переменных двойственного функционирования m(t) для вершин выходного слоя 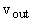 . Тогда для любого qÎ . Тогда для любого qÎ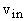
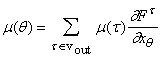 . . |
(11) |
где 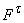 - соответствующая
вершине t функция от
независимых переменных и констант, отмечающих вершины нулевого слоя G,
- соответствующая
вершине t функция от
независимых переменных и констант, отмечающих вершины нулевого слоя G, 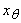 - соответствующая
вершине qÎ
- соответствующая
вершине qÎ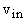 переменная или константа, а производные в (11) берутся при
фиксированных значениях прочих переменных и констант.
переменная или константа, а производные в (11) берутся при
фиксированных значениях прочих переменных и констант.
Доказательство
проводится индукцией по числу слоев. Для графов из двух слоев - нулевого и
первого - теорема очевидна. Спуск от i+1-слойных графов к i-слойным производится с помощью формулы 5.
| а) |
б) |
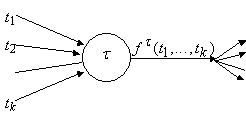 |
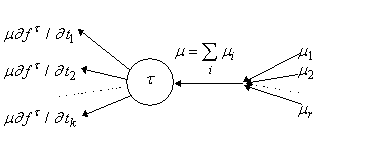 |
| Рис. 3. Прохождение вершины t
в прямом (а) и обратном (б) направлении. |
Прохождение вершины графа и
прилегающих к ней ребер при прямом и обратном процессах проиллюстрировано на
рис. 3.
5. Сложность вычисления функции и ее градиента
Подсчитаем теперь число операций,
необходимых для вычисления всех двойственных переменных m(t) для вершин и m(t¢,t)
- для ребер.
Во-первых, нужно вычислить все
частные производные
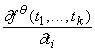
для всех вершин q и всех k аргументов «простой»
функции, соответствующей каждой вершине. Число таких производных равно сумме
числа аргументов для всех функциональных символов, соответствующих вершинам
графа, то есть следующей величине E:
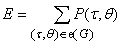 . .
Договоримся в этом
разделе отображать ребра (t¢,t), имеющие в своих метках P(t¢,t)
больше одного номера, как пучки ребер, идущих от вершины t¢
к вершине t - по одному такому
ребру для каждого номера из P(t¢,t). Число E просто равно числу
ребер в графе. Число необходимых умножений и число сложений также не
превосходят E.
Количество вычислений «простых»
функций при вычислении сложной равно числу вершин графа. Обозначим его V. Отношение E/V дает представление об отношении вычислительных затрат на
вычисление градиента к затратам на вычисление функции. Чтобы последовательно
использовать эту оценку, а также искать те функции, для которых вычисление
градиента еще проще, необходимо зафиксировать исходные предположения. Будем
обозначать Tf затраты на вычисление f.
- Для каждой вершины графа, соответствующей ей функции f, и любого аргумента этой функции x
справедлива оценка
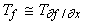 ; ;
- Для функций f=
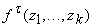 ,
соответствующих вершинам графа, ,
соответствующих вершинам графа, 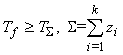 , то есть сумма переменных - простейшая функция;
, то есть сумма переменных - простейшая функция;
- Умножение и сложение имеют примерно одинаковую сложность.
В предположениях 1-3 зафиксирован
тот уровень точности, с которым будут делаться оценки. При формальном
использовании отношения «a примерно
равно b» неизбежны
парадоксы типа «куча»: один камень не куча, если n камней -
не куча, то и n+1 - тоже, следовательно... . Чтобы
избежать этого и сделать рассуждения более наглядными, поступим следующим
образом. Сложность «простой» функции k переменных
и любой ее частной производной оценим как ck, где c - некоторая константа, c³1;
сложность суммы k слагаемых (и произведения k сомножителей) определим как k-1.
Последнее вычитание единицы имеет смысл при рассмотрении большого числа сумм,
содержащих мало слагаемых.
Пусть, как и выше, E- число ребер графа, V- число вершин, Vout - число выходных вершин (им не
соответствует ни одной суммы в (6)). Сложность
прямого прохождения графа (вычисления функций) оценивается как cE.
Обратное прохождение графа при
вычислении градиентов складывается из трех слагаемых:
- Вычисление всех частных производных простых функций,
соответствующих вершинам графа. Необходимо вычислить E таких
производных. Сложность вычисления одной такой производной для вершины t, имеющей |in(t)| входящих ребер,
оценивается как c|in(t)|. Оценка сложности
вычисления всех этих производных дается следующей суммой TDif= c
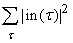 (
(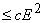 ). ).
- Вычисление всех произведений (7) на ребрах - E произведений (в связи с тем, что мы в данном разделе передачу
сигнала на разные входы автомата, вычисляющего
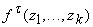 , обозначаем различными ребрами, уравнения (7), сохраняя
прежнюю внешнюю форму, преобразуются так, что в суммах остается по одному
слагаемому, остальное суммирование переносится к вершинам (6)). , обозначаем различными ребрами, уравнения (7), сохраняя
прежнюю внешнюю форму, преобразуются так, что в суммах остается по одному
слагаемому, остальное суммирование переносится к вершинам (6)).
- Вычисление всех сумм (6) - сложность равна E‑(V‑ Vout).
Итого, полная сложность обратного
прохождения сигналов оценивается как
T= TDif+2 E‑(V‑ Vout)= c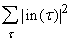 +2 E‑(V‑ Vout).
+2 E‑(V‑ Vout).
Основную роль в последней сумме
играет первое слагаемое - именно им определяется сложность обратного
распространения по графу (если все |in(t)|=1, то TDif =cE, а уже в
случае, когда |in(t)|=2, мы получаем TDif =2cE). Поэтому можно положить T»TDif (строго говоря, 3TDif³T³TDif , однако различия в два-три
раза для нас сейчас несущественны).
Если характерное число переменных у
простых функций, соответствующих вершинам графа, равно m (то есть |in(t)|=m), то для вычисляемой по графу сложной функции F можно оценить отношение затрат на вычисление F и gradF
следующим образом:
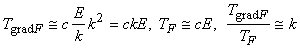 . .
Эта оценка, конечно, лучше, чем
полное число переменных n, но все же искомое отношение
оценивается примерно как отношение числа ребер к числу вершин E/V (с
точностью до менее значимых слагаемых). Если нас интересуют графы с большим
числом связей, то для сохранения эффективности вычисления градиентов нужно
ограничиваться специальными классами простых функций. Из исходных предположений
1-3 наиболее существенно первое (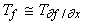 ). Зададимся вопросом: для каких функций f
вычисление частных производных вообще не требует вычислений? ). Зададимся вопросом: для каких функций f
вычисление частных производных вообще не требует вычислений?
Ответ очевиден: общий вид таких
функций
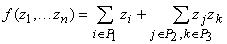 , , |
(12) |
где множества
индексов P1, P2,
P3 не
пересекаются и, кроме того, P2, P3 имеют одинаковое число элементов. Значения всех
частных производных таких функций уже известны, а источники (адреса) этих
значений указываются связями графа. Какие-то значения zk во
второй сумме могут быть константами (значения нулевого слоя), какие-то -
независимыми переменными (также нулевой слой) или значениями, найденными при
промежуточных вычислениях.
В общем случае функции (12)
билинейны. Их частный случай - линейные функции: если индексам из P2 в (12) соответствуют константы, то функция f - линейная.
И функции вида (12), и
соответствующие им вершины будем называть квазилинейными.
Пусть интерпретация функциональных
символов такова, что в графе вычислений присутствуют только вершины двух
сортов: квазилинейные или с одной входной связью (соответствующие простым
функциям одного переменного). Обозначим количества этих вершин Vq
и V1 соответственно. Оценка сложности вычисления
градиента для таких графов принципиально меняется. Обратное функционирование в
этом случае требует следующих затрат:
- Поиск всех производных функций одного переменного, соответствующих вершинам графа (число таких
производных равно V1), сложность поиска
одной производной оценивается как c.
- Вычисление всех произведений (7) на ребрах - E произведений.
- Вычисление всех сумм (6) - сложность равна E‑(V‑ Vout).
Итого, суммарная сложность
обратного прохождения сигналов оценивается как
TgradF = cV1+2E‑(V‑
Vout).
Оценим сложность вычислений при
прямом распространении:
- Для любой квазилинейной
вершины t сложность вычисления
функции оценивается как |in(t)|-1,
- Для любой вершины с одной
входной связью сложность оценивается как c.
Итак, для прямого распространения
сложность оценивается как
TF=cV1+(E‑ V1‑ Vq).
С ростом числа связей 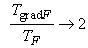 !!!
!!!
Графы вычислений (с заданной
интерпретацией функциональных символов), в которых присутствуют только вершины
двух сортов: квазилинейные или с одной входной связью (соответствующие простым
функциям одного переменного) играют особую роль. Будем называть их существенно
квазилинейными. Для функций, вычисляемых с помощью таких графов,
затраты на вычисление вектора градиента примерно вдвое больше, чем затраты на
вычисление значения функции (всего!). При этом число связей и отношение 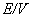 могут быть сколь угодно большими. Это достоинство делает
использование существенно квазилинейных графов весьма притягательным во всех
задачах оптимизации. Их частным случаем являются нейронные сети, для которых
роль квазилинейных вершин играют адаптивные линейные сумматоры.
могут быть сколь угодно большими. Это достоинство делает
использование существенно квазилинейных графов весьма притягательным во всех
задачах оптимизации. Их частным случаем являются нейронные сети, для которых
роль квазилинейных вершин играют адаптивные линейные сумматоры.
Таким образом, обратное прохождение
адаптивного сумматора требует таких же затрат, как и прямое. Для других
элементов стандартного нейрона обратное распространение строится столь же
просто: точка ветвления при обратном процессе превращается в простой сумматор,
а нелинейный преобразователь 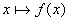 в линейную связь
в линейную связь 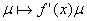 с коэффициентом связи
с коэффициентом связи
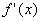 . Поэтому для нейронных сетей обратное распространение
выглядит особенно просто. Детали можно найти в различных руководствах, например
[5,6] . Поэтому для нейронных сетей обратное распространение
выглядит особенно просто. Детали можно найти в различных руководствах, например
[5,6]
Отличие общего случая от более
привычных нейронных сетей состоит в том, что можно использовать билинейные
комбинации (12) произвольных уже вычисленных функций, а не только линейные
функции от них с постоянными коэффициентами-весами.
В определенном смысле квазилинейные
функции (12) вычисляются линейными сумматорами с весами 1 и 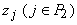 и аргументами
и аргументами 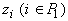 и
и 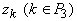 , только веса не обязательно являются константами, а могут
вычисляться на любом слое. , только веса не обязательно являются константами, а могут
вычисляться на любом слое.
Естественно возникает вопрос о
вычислительных возможностях сетей, все вершины которых являются квазилинейными.
Множество функций, вычисляемых такими сетями, содержит все координатные функции
и замкнуто относительно сложения, умножения на константу и умножения функций.
Следовательно оно содержит и все многочлены от любого количества переменных.
Любая непрерывная функция на замкнутом ограниченном множестве в конечномерном
пространстве может быть сколь угодно точно приближена с их помощью.
6. Двойственность по Лежандру и смысл двойственных переменных
Просматривая текст предыдущих
разделов, я убедился, что подробное изложение и элементы стиля математической
логики могут даже очевидное сделать сложным. В данном разделе описывается связь
двойственного функционирования сетей автоматов с преобразованием Лежандра и
неопределенными множителями Лагранжа. Это изложение ориентировано на читателя,
знакомившегося с лагранжевым и гамильтоновым формализмами и их связью (в классической
механике или вариационном исчислении). Фактически на двух страницах будет
заново изложен весь предыдущий материал главы.
Переменные обратного
функционирования m появляются как
вспомогательные при вычислении производных сложной функции. Переменные такого
типа появляются не случайно. Они постоянно возникают в задачах оптимизации и
являются множителями Лагранжа.
Мы вводим m,
исходя из правил дифференцирования сложной функции. Возможен другой путь,
связанный с переходом от функции Лагранжа к функции Гамильтона. Изложим его и
параллельно получим ряд дальнейших обобщений. Для всех сетей автоматов,
встречавшихся нам в предыдущих разделах и главах, можно выделить три группы
переменных:
внешние входные сигналы x...,
переменные функционирования - значения на выходах всех элементов сети f...,
переменные
обучения a...
(многоточиями заменяются различные наборы индексов).
Объединим их в две группы -
вычисляемые величины y...
- значения f...
и задаваемые - b...
(включая a... и x...). Упростим индексацию,
перенумеровав f и b натуральными числами: f1,...,fN ; b1 ,...,bM .
Пусть функционирование системы
задается набором из N уравнений
| yi(y1,...,yN ,b1 ,...,bM)=0 (i =1,...,N). |
(13) |
Для послойного вычисления сложных
функций вычисляемые переменные - это значения вершин для всех слоев, кроме
нулевого, задаваемые переменные - это значения вершин первого слоя (константы и
значения переменных), а уравнения функционирования имеют простейший вид (4),
для которого
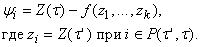
Предполагается, что система уравнений
(13) задает способ вычисления yi .
Пусть имеется функция (лагранжиан) H(y1,...,yN,b1 ,...,bM). Эта функция
зависит от b и явно, и неявно - через
переменные функционирования y. Если
представить, что уравнения (13) разрешены относительно всех y (y=y(b)),
то H можно представить как функцию от
b:
| H=H1(b)=H(y1(b),...,yN(b),b). |
(14) |
где b - вектор с компонентами bi .
Для задачи обучения требуется найти
производные Di=¶H1(b)/¶bi . Непосредственно
и явно это сделать трудно.
Поступим по-другому. Введем новые
переменные m1,...,mN (множители
Лагранжа) и производящую функцию W:
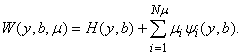
В функции W аргументы y, b и m
- независимые переменные.
Уравнения (13) можно записать как
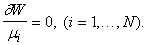 |
(15) |
Заметим, что для тех y, b, которые удовлетворяют уравнениям
(13), при любых m
Это означает, что для истинных
значений переменных функционирования y
при данных b функция W(y,b,m)
совпадает с исследуемой функцией H.
Попытаемся подобрать такую
зависимость mi(b), чтобы, используя (16), получить для Di=¶H1(b)/¶bi наиболее простые
выражения . На многообразии решений (15)
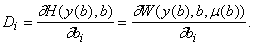
Поэтому
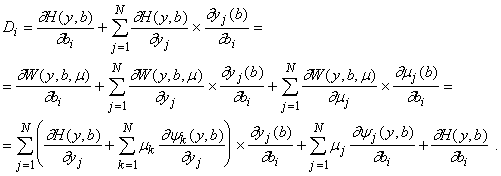 |
(17) |
Мы всюду различаем функцию H(y,b), где y и b - независимые
переменные, и функцию только от переменных b
H(y(b),b), где y(b) определены из
уравнений (13). Аналогичное различение принимается для функций W(y,b,m)
и W(y(b),b,m (b)).
Произвол в определении m(b) надо
использовать наилучшим образом - все равно от него придется избавляться, доопределяя
зависимости. Если выбрать такие m,
что слагаемые в первой сумме последней строки выражения (17) обратятся в нуль,
то формула для Di
резко упростится. Положим поэтому
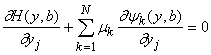 . . |
(18) |
Это - система уравнений для
определения mk
(k=1,...,N). Если m
определены согласно (18), то
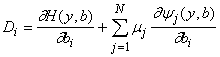
это - в точности те
выражения, которые использовались при поиске производных сложных функций. В
наших вычислениях мы пользовались явным описанием функционирования. Метод
множителей Лагранжа допускает и менее явные описания сетей.
В математическом фольклоре бытует
такой тезис: сложная задача оптимизации может быть решена только при
эффективном использовании двойственности. Методы быстрого дифференцирования
являются яркой иллюстрацией этого тезиса.
7. Оптимизационное обучение нейронных сетей
Когда можно представить обучение
нейронных сетей как задачу оптимизации? В тех случаях, когда удается оценить работу сети. Это означает, что
можно указать, хорошо или плохо сеть решает поставленные ей задачи и оценить
это «хорошо или плохо» количественно. Строится функция оценки. Она, как правило, явно зависит от выходных сигналов
сети и неявно (через функционирование) - от всех ее параметров. Простейший и
самый распространенный пример оценки - сумма квадратов расстояний от выходных
сигналов сети до их требуемых значений:
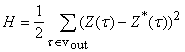 , ,
где 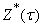 - требуемое значение
выходного сигнала.
- требуемое значение
выходного сигнала.
Другой пример оценки- качество
классификации в сетях Кохонена. В этом случае ответы заранее неизвестны, но
качество работы сети оценить можно.
Устройство, вычисляющее оценку,
надстраивается над нейронной сетью и градиент оценки может быть вычислен с
использованием описанного принципа двойственности.
В тех случаях, когда оценка
является суммой квадратов ошибок, значения независимых переменных двойственного
функционирования m(t)
для вершин выходного слоя 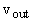 при вычислении
градиента H устанавливаются
равными
при вычислении
градиента H устанавливаются
равными
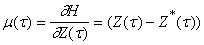 |
(19) |
на вход при
обратном функционировании поступают ошибки выходных сигналов! Это
обстоятельство настолько впечатлило исследователей, что они назвали метод
вычисления градиента оценки методом обратного распространения ошибок. Впрочем,
после формулы Уидроу, описанной в главе 2, формула (19) должна быть очевидной.
Для обучения используется оценка,
усредненная по примерам с известным ответом.
Предлагается рассматривать обучение
нейронных сетей как задачу оптимизации. Это означает, что весь мощный арсенал
методов оптимизации может быть испытан для обучения. Так и видится:
нейрокомпьютеры наискорейшего спуска, нейрокомпьютеры Ньютона, Флетчера и т.п.
- по названию метода нелинейной оптимизации.
Существует, однако, ряд специфических ограничений. Они связаны с
огромной размерностью задачи обучения. Число параметров может достигать 108 - и даже
более. Уже в простейших программных имитаторах на персональных компьютерах
подбирается 103
- 104
параметров.
Из-за высокой размерности возникает
два требования к алгоритму:
1. Ограничение по памяти. Пусть n - число параметров. Если алгоритм
требует затрат памяти порядка n2 ,то он вряд
ли применим для обучения. Вообще говоря, желательно иметь алгоритмы, которые
требуют затрат памяти порядка Kn, K=const.
2. Возможность параллельного
выполнения наиболее трудоемких этапов алгоритма и желательно - нейронной сетью.
Если какой-либо особо привлекательный алгоритм требует память порядка n2 , то его все же можно использовать,
если с помощью анализа чувствительности и, возможно, контрастирования сократить
число обучаемых параметров до разумных пределов.
Еще два обстоятельства связаны с
нейрокомпьютерной спецификой.
1. Обученный нейрокомпьютер должен
с приемлемой точностью решать все тестовые задачи (или, быть может, почти все с
очень малой частью исключений). Поэтому задача обучения становится по существу
многокритериальной задачей оптимизации: надо найти точку общего минимума
большого числа функций. Обучение нейрокомпьютера исходит из гипотезы о
существовании такой точки. Основания гипотезы - очень большое число переменных
и сходство между функциями. Само понятие "сходство" здесь трудно
формализовать, но опыт показывает что предположение о существовании общего
минимума или, точнее, точек, где значения всех оценок мало отличаются от
минимальных, часто оправдывается.
2. Обученный нейрокомпьютер должен
иметь возможность приобретать новые навыки без утраты старых. Возможно более
слабое требование: новые навыки могут сопровождаться потерей точности в старых,
но эта потеря не должна быть особо существенной, а качественные изменения
должны быть исключены. Это означает, что в достаточно большой окрестности
найденной точки общего минимума оценок значения этих функций незначительно
отличаются от минимальных. Мало того, что должна быть найдена точка общего
минимума, так она еще должна лежать в достаточно широкой низменности, где
значения всех минимизируемых функций близки к минимуму. Для решения этой задачи
нужны специальные средства.
Итак, имеем четыре специфических
ограничения, выделяющих обучение нейрокомпьютера из общих задач оптимизации:
астрономическое число параметров, необходимость высокого параллелизма при
обучении, многокритериальность решаемых задач, необходимость найти достаточно
широкую область, в которой значения всех минимизируемых функций близки к
минимальным. В остальном - это просто задача оптимизации и многие классические
и современные методы достаточно естественно ложатся на структуру нейронной
сети.
Заметим, кстати, что если вести
оптимизацию (минимизацию ошибки), меняя параметры сети, то в результате получим
решение задачи аппроксимации. Если же ведется минимизация целевой некоторой
функции и ищутся соответствующие значения переменных, то в результате решаем
задачу оптимизации (хотя формально это одна и та же математическая задача и
разделение на параметры и переменные определяется логикой предметной области, а
с формальной точки зрения разница практически отсутствует).
Значительное число публикаций по
методам обучения нейронных сетей посвящено переносу классических алгоритмов
оптимизации (см., например, [7,8]) на нейронные сети или поиску новых редакций
этих методов, более соответствующих описанным ограничениям - таких, например,
как метод виртуальных частиц [5,6]. Существуют обширные обзоры и курсы,
посвященные обучению нейронных сетей (например, [9,10]). Не будем здесь останавливаться
на обзоре этих работ - если найден градиент, то остальное приложится.
Работа над главой была поддержана Красноярским краевым фондом науки, грант 6F0124.
Литература
- Rumelhart D.E., Hinton G.E., Williams R.J.
Learning internal representations by error propagation. // Parallel Distributed
Processing: Exploration in the Microstructure of Cognition, D.E.Rumelhart and
J.L.McClelland (Eds.), vol. 1, Cambridge, MA: MIT Press, 1986. PP. 318 - 362.
- Rummelhart D.E., Hinton G.E., Williams R.J. Learning representations by
back-propagating errors // Nature, 1986. V. 323. P. 533-536.
- Барцев С.И., Охонин В.А. Адаптивные сети обработки информации. Препринт ИФ СО АН СССР,
Красноярск, 1986, №59Б, 20 c.
- Шенфилд Дж. Математическая логика. М.: Наука, 1975. 528 с.
- Горбань А.Н. Обучение нейронных сетей. М.": изд. СССР-США СП "ПараГраф",
1990. 160 с. (English Translation: AMSE
Transaction, Scientific Siberian, A, 1993, Vol. 6. Neurocomputing, РP. 1-134).
- Горбань А.Н., Россиев Д.А. Нейронные сети на персональном компьютере. Новосибирск:
Наука (Сиб. отделение), 1996. 276 с.
- Химмельблау Д. Прикладное нелинейное программирование. М.: Мир, 1975. 534 с.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. М.: Мир,1985. 509 с.
- Zurada J. M. Introduction to artificial neural systems. PWS Publishing Company, 1992. 785 pp.
- Haykin S. Neural networks. A comprehensive foundations. McMillan College Publ. Co. N.Y., 1994. 696 pp.
1 660036, Красноярск-36, ВЦК СО РАН. E-mail:
2 Трудно удержаться от вольности речи - обращения к формально еще не введенной, но совершенно очевидной интерпретации («... обозначающие...»).
|
 материалы
материалы  справочник
справочник  форум
форум  гостевая
гостевая  ссылки
ссылки