|
1. Нейробум: поэзия и проза нейронных сетей
В словах «искусственные нейронные сети» слышатся
отзвуки фантазий об андроидах и бунте роботов, о машинах, заменяющих и
имитирующих человека. Эти фантазии интенсивно поддерживаются многими
разработчиками нейросистем: рисуется не очень отдаленное будущее, в котором
роботы осваивают различные виды работ, просто наблюдая за человеком, а в более
отдаленной перспективе – человеческое сознание и личность перегружаются в
искусственную нейронную сеть – появляются шансы на вечную жизнь.
Поэтическая игра воображения вовлекает в работу
молодежь, поэзия рекламы создает научную моду и влияет на финансовые вложения.
Можете ли Вы четко различить, где кончается бескорыстная творческая игра и
начинается реклама? У меня такое однозначное различение не получается: это как
вопрос о искренности – можно сомневаться даже в своей собственной искренности.
Итак: игра и мода как важные движущие силы.
В словах «модное научное направление» слышится нечто
неоднозначное ‑ то ли пренебрежение, смешанное с завистью, то ли еще
что-то. А вообще, мода в науке – это хорошо или плохо? Дадим три ответа на этот
вопрос.
1. Мода – это хорошо!
Когда в науке появляется новая мода, тысячи исследователей, грустивших над
старыми темами, порядком надоевшими еще со времени писания диссертации, со
свежим азартом бросаются в дело. Новая мода позволяет им освободиться от личной
истории.
Мы все зависим от своего прошлого, от привычных дел
и привычных мыслей. Так давайте же приветствовать все, что освобождает нас от
этой зависимости! В новой модной области почти нет накопленных преимуществ –
все равны. Это хорошо для молодежи.
2. Мода – это плохо! Она
противоречит глубине и тщательности научного поиска. Часто "новые"
результаты, полученные в погоне за модой, суть всего-навсего хорошо забытые
старые, да еще нередко и перевранные. Погоня за модой растлевает, заставляет
переписывать старые работы и в новой словесной упаковке выдавать их за свои.
Мода ‑ источник сверххалтуры. Примеров тому – тысячи.
"Гений – это терпение мысли." Так давайте
же вслед за Ньютоном и другими Великими культивировать в себе это терпение. Не
будем поддаваться соблазну моды.
3. Мода в науке – это элемент реальности. Так повелось во второй половине XX века: наука
стала массовой и в ней постоянно вспыхивают волны моды. Можно ли относиться к
реальности с позиций должного: так, дескать, должно быть, а этак – нет?
Наверное, можно, но это уж точно непродуктивно. Волны моды и рекламные кампании
стали элементом организации массовой науки и с этим приходится считаться,
нравится нам это или нет.
Нейронные сети нынче в моде и поэтическая реклама
делает свое дело, привлекает внимание. Но стоит ли следовать за модой? Ресурсы
ограничены – особенно у нас, особенно теперь. Все равно всего на всех не
хватит. И возникают вопросы:
- нейрокомпьютер – это интеллектуальная игрушка или новая техническая революция?
- что нового и полезного может сделать нейрокомпьютер?
За этими вопросами скрыты два базовых предположения:
- на новые игрушки, даже высокоинтеллектуальные, средств нет;
- нейрокомпьютер должен доказать свои новые возможности – сделать то,
чего не может сделать обычная ЭВМ, – иначе на него не стоит тратиться.
У энтузиастов есть свои рекламные способы отвечать
на заданные вопросы, рисуя светлые послезавтрашние горизонты. Но все это в
будущем. А сейчас? Ответы парадоксальны:
- нейрокомпьютеры – это новая техническая революция, которая приходит к нам в виде интеллектуальной игрушки (вспомните – и
персональные ЭВМ были придуманы для игры!);
- для любой задачи, которую может решить нейрокомпьютер, можно построить более стандартную специализированную ЭВМ,
которая решит ее не хуже, а чаще всего – даже лучше.
Зачем же тогда нейрокомпьютеры? Вступая в творческую
игру, мы не можем знать, чем она кончится, иначе это не Игра. Поэзия и реклама
дают нам фантом, призрак результата, погоня за которым ‑ важнейшая часть
игры. Столь же призрачными могут оказаться и прозаичные ответы ‑ игра
может далеко от них увести. Но и они необходимы ‑ трудно бегать по
облакам и иллюзия практичности столь же важна, сколь и иллюзия величия. Вот
несколько вариантов прозаичных ответов на вопрос «зачем?» ‑ можно
выбрать, что для Вас важнее:
А. Нейрокомпьютеры дают стандартный способ решения
многих нестандартных задач. И неважно, что специализированная машина лучше
решит один класс задач. Важнее, что один нейрокомпьютер решит и эту задачу, и
другую, и третью – и не надо каждый раз проектировать специализированную ЭВМ –
нейрокомпьютер сделает все сам и почти не хуже.
Б. Вместо программирования – обучение.
Нейрокомпьютер учится – нужно только формировать учебные задачники. Труд
программиста замещается новым трудом – учителя (может быть, надо сказать –
тренера или дрессировщика). Лучше это или хуже? Ни то, ни другое. Программист
предписывает машине все детали работы, учитель – создает "образовательную
среду", к которой приспосабливается нейрокомпьютер. Появляются новые
возможности для работы.
В. Нейрокомпьютеры особенно эффективны там, где
нужно подобие человеческой интуиции – для распознавания образов (узнавания лиц,
чтения рукописных текстов), перевода с одного естественного языка на другой и
т.п. Именно для таких задач обычно трудно сочинить явный алгоритм.
Г. Гибкость структуры: можно различными способами
комбинировать простые составляющие нейрокомпьютеров – нейроны и связи между
ними. За счет этого на одной элементной базе и даже внутри "тела"
одного нейрокомпьютера можно создавать совершенно различные машины. Появляется
еще одна новая профессия – "нейроконструктор" (конструктор мозгов).
Д. Нейронные сети позволяют создать эффективное
программное обеспечение для высокопараллельных компьютеров. Для
высокопараллельных машин хорошо известна проблема: как их эффективно
использовать – как добиться, чтобы все элементы одновременно и без лишнего
дублирования вычисляли что-нибудь полезное? Создавая математическое обеспечения
на базе нейронных сетей, можно для широкого класса задач решить эту проблему.
Если перейти к еще более прозаическому уровню
повседневной работы, то нейронные сети ‑ это всего-навсего сети,
состоящие из связанных между собой простых элементов ‑ формальных
нейронов. Значительное большинство работ по нейроинформатике посвящено переносу
различных алгоритмов решения задач на такие сети.
Ядром используемых представлений является идея о
том, что нейроны можно моделировать довольно простыми автоматами, а вся
сложность мозга, гибкость его функционирования и другие важнейшие качества
определяются связями между нейронами. Каждая связь представляется как совсем
простой элемент, служащий для передачи сигнала. Предельным выражением этой
точки зрения может служить лозунг: "структура связей – все, свойства
элементов – ничто".
Совокупность идей и научно-техническое направление,
определяемое описанным представлением о мозге, называется коннекционизмом
(по-ангийски connection – связь). Как все это соотносится с реальным мозгом?
Так же, как карикатура или шарж со своим прототипом-человеком ‑ весьма
условно. Это нормально: важно не буквальное соответствие живому прототипу, а
продуктивность технической идеи.
С коннекционизмом тесно связан следующий блок идей:
- однородность системы (элементы одинаковы и чрезвычайно просты, все определяется структурой связей);
- надежные системы из ненадежных элементов и "аналоговый ренессанс" – использование простых
аналоговых элементов;
- "голографические" системы – при разрушении случайно выбранной части система сохраняет свои
полезные свойства.
Предполагается, что система связей достаточно богата
по своим возможностям и достаточно избыточна, чтобы скомпенсировать бедность
выбора элементов, их ненадежность, возможные разрушения части связей.
Коннекционизм и связанные с ним идеи однородности,
избыточности и голографичности еще ничего не говорят нам о том, как же такую
систему научить решать реальные задачи. Хотелось бы, чтобы это обучение
обходилось не слишком дорого.
На первый взгляд кажется, что коннекционистские
системы не допускают прямого программирования, то есть формирования связей по
явным правилам. Это, однако, не совсем так. Существует большой класс задач:
нейронные системы ассоциативной памяти, статистической обработки, фильтрации и
др., для которых связи формируются по явным формулам. Но еще больше (по объему
существующих приложений) задач требует неявного процесса. По аналогии с
обучением животных или человека этот процесс мы также называем обучением.
Обучение обычно строится так: существует задачник –
набор примеров с заданными ответами. Эти примеры предъявляются системе. Нейроны
получают по входным связям сигналы – "условия примера", преобразуют
их, несколько раз обмениваются преобразованными сигналами и, наконец, выдают
ответ – также набор сигналов. Отклонение от правильного ответа штрафуется.
Обучение состоит в минимизации штрафа как (неявной) функции связей. Примерно
четверть нашей книги состоит в описании техники такой оптимизации и возникающих
при этом дополнительных задач.
Неявное обучение приводит к тому, что структура
связей становится "непонятной" – не существует иного способа ее
прочитать, кроме как запустить функционирование сети. Становится сложно
ответить на вопрос: "Как нейронная сеть получает результат?" – то
есть построить понятную человеку логическую конструкцию, воспроизводящую
действия сети.
Это явление
можно назвать "логической непрозрачностью" нейронных сетей, обученных
по неявным правилам. В работе с логически непрозрачными нейронными сетями
иногда оказываются полезными представления, разработанные в психологии и
педагогике, и обращение с обучаемой сетью как с дрессируемой зверушкой или с
обучаемым младенцем – это еще один источник идей. Возможно, со временем
возникнет такая область деятельности – "нейропедагогика" – обучение
искусственных нейронных сетей.
С другой
стороны, при использовании нейронных сетей в экспертных системах на PC
возникает потребность прочитать и логически проинтерпретировать навыки,
выработанные сетью. В главе 9 описаны служащие для этого методы
контрастирования – получения неявными методами логически прозрачных нейронных
сетей. Однако за логическую прозрачность приходится платить снижением
избыточности, так как при контрастировании удаляются все связи кроме самых
важных, без которых задача не может быть решена.
Итак, очевидно наличие двух источников идеологии
нейроинформатики. Это представления о строении мозга и о процессах обучения.
Существуют группы исследователей и научные школы, для которых эти источники
идей имеют символическое, а иногда даже мистическое или тотемическое значение.
Но это все поэзия, а мы пока перейдем к прозе ‑ к изучению формальных
нейронов.
2. Элементы нейронных сетей
Для описания алгоритмов и устройств в
нейроинформатике выработана специальная "схемотехника", в которой
элементарные устройства – сумматоры, синапсы, нейроны и т.п. объединяются в
сети, предназначенные для решения задач.
Интересен статус этой схемотехники – для многих
начинающих кажется неожиданным, что ни в аппаратной реализации нейронных сетей,
ни в профессиональном программном обеспечении все эти элементы вовсе не
обязательно реализуются как отдельные части или блоки. Используемая в
нейроинформатике идеальная схемотехника представляет собой особый язык для
представления нейронных сетей и их обуждения. При программной и аппаратной
реализации выполненные на этом языке описания переводятся на языки другого
уровня, более пригодные для реализации.
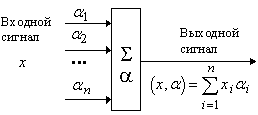
Самый заслуженный и, вероятно, наиболее важный
элемент нейросистем – это адаптивный
сумматор. Адаптивный сумматор вычисляет скалярное произведение вектора
входного сигнала x на вектор параметров a.
На схемах будем обозначать его так, как показано на рис. 1. Адаптивным называем его из-за наличия вектора
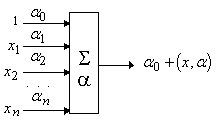
настраиваемых параметров a. Для многих задач полезно
иметь линейную неоднородную функцию выходных сигналов. Ее вычисление также
можно представить с помощью адаптивного сумматора, имеющего n+1
вход и получающего на 0-й вход постоянный единичный сигнал (рис. 2).
 |
|
 |
| Рис. 1. Адаптивный сумматор |
|
Рис. 2. Неоднородный адаптивный сумматор |
 |
|
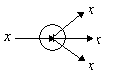 |
| Рис. 3. Нелиней-ный преобразова-тель сигнала |
|
Рис. 4. Точка ветвления |
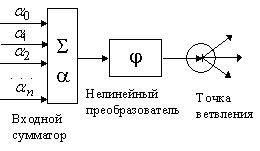 |
| Рис. 5. Формальный нейрон |
Нелинейный преобразователь сигнала
изображен на рис. 3. Он получает скалярный входной сигнал x и переводит его в j(x).
Точка ветвления служит для рассылки одного
сигнала по нескольким адресам (рис. 4). Она получает скалярный входной сигнал x
и передает его всем своим выходам. Стандартный
формальный нейрон составлен из входного сумматора, нелинейного
преобразователя и точки ветвления на выходе (рис. 5).
Линейная связь ‑ синапс ‑
отдельно от сумматоров не встречается, однако для некоторых рассуждений бывает
удобно выделить этот элемент (рис. 6). Он умножает входной сигнал
x на «вес синапса» a.
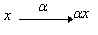 |
| Рис. 6. Синапс |
Также бывает полезно «присоединить» связи не ко
входному сумматору, а к точке ветвления. В результате получаем элемент,
двойственный адаптивному сумматору и называемый «выходная звезда». Его выходные связи производят умножение сигнала
на свои веса.
Итак, дано описание основных элементов, из которых
составляются нейронные сети.
3. Архитектура нейронных сетей
Перейдем теперь к вопросу: как можно составлять эти
сети? Строго говоря, как угодно, лишь бы входы получали какие-нибудь сигналы.
Но такой произвол слишком необозрим, поэтому используют несколько стандартных
архитектур, из которых путем вырезания лишнего или (реже) добавления строят
большинство используемых сетей.
Сначала следует договориться о том, как будет
согласована работа различных нейронов во времени. Как только в системе
возникает более одного элемента, встает вопрос о синхронности функционирования.
Для привычных нам всем программных имитаторов нейронных сетей на цифровых ЭВМ
такого вопроса нет только из-за свойств основного компьютера, на котором реализуются
нейронные сети. Для других способов реализации такой вопрос весьма важен. Все
же здесь и далее рассматриваются только нейронные сети, синхронно
функционирующие в дискретные моменты времени: все нейроны срабатывают «разом».
В зоопарке нейронных сетей можно выделить две
базовых архитектуры – слоистые и полносвязные сети.
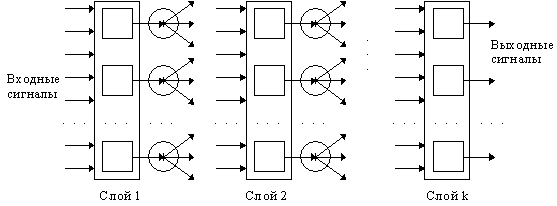 |
| Рис. 7. Слоистая сеть |
Слоистые сети: нейроны расположены в
несколько слоев (рис. 7). Нейроны первого слоя получают входные сигналы,
преобразуют их и через точки ветвления передают нейронам второго слоя. Далее
срабатывает второй слой и т.д. до k-го
слоя, который выдает выходные сигналы для интерпретатора и пользователя. Если
не оговорено противное, то каждый выходной сигнал i-го слоя подается на вход всех нейронов i+1-го.
Число нейронов в каждом слое может быть любым и никак
заранее не связано с количеством нейронов в других слоях. Стандартный способ
подачи входных сигналов: все нейроны первого слоя получают каждый входной
сигнал. Особое распространение получили трехслойные сети, в которых каждый слой
имеет свое наименование: первый – входной, второй – скрытый, третий – выходной.
Полносвязные сети:
каждый нейрон передает свой выходной сигнал остальным нейронам, включая самого
себя. Выходными сигналами сети могут быть все или некоторые выходные сигналы
нейронов после нескольких тактов функционирования сети. Все входные сигналы
подаются всем нейронам.
Элементы слоистых и полносвязных сетей могут
выбираться по-разному. Существует, впрочем, стандартный выбор – нейрон с
адаптивным неоднородным линейным сумматором на входе (рис. 5).
Для полносвязной сети входной сумматор нейрона
фактически распадается на два: первый вычисляет линейную функцию от входных
сигналов сети, второй – линейную функцию от выходных сигналов других нейронов,
полученных на предыдущем шаге.
Функция активации нейронов (характеристическая функция)
j –
нелинейный преобразователь, преобразующий выходной сигнал сумматора (см. рис. 5) – может
быть одной и той же для всех нейронов сети. В этом случае сеть называют однородной (гомогенной).
Если же j зависит еще от одного или нескольких
параметров, значения которых меняются от нейрона к нейрону, то сеть называют неоднородной (гетерогенной).
Составление сети из нейронов стандартного вида (рис. 5) не является обязательным. Слоистая или
полносвязная архитектуры не налагают
существенных ограничений на участвующие в них элементы. Единственное жесткое
требование, предъявляемое архитектурой к элементам сети, это соответствие
размерности вектора входных сигналов элемента (она определяется архитектурой)
числу его входов.
Если полносвязная сеть функционирует до получения
ответа заданное число тактов k, то ее
можно представить как частный случай k-слойной
сети, все слои которой одинаковы и каждый из них соответствует такту
функционирования полносвязной сети.
Существенное различие между полносвязной и слоистой
сетями возникает тогда, когда число тактов функционирования заранее не
ограничено – слоистая сеть так работать не может.
4. Существуют ли функции многих переменных?
Вопрос, вынесенный в заголовок раздела, естественно
возникает при изучении возможностей нейронных сетей. Из схем предыдущих
разделов видно, что нейронные сети вычисляют линейные функции, нелинейные
функции одного переменного, а также
всевозможные суперпозиции ‑ функции от функций, получаемые при каскадном
соединении сетей. Что можно получить, используя только такие операции? Какие
функции удастся вычислить точно, а какие функции можно сколь угодно точно
аппроксимировать с помощью нейронных сетей? Чтобы изучить возможности нейронных
сетей, нужно ответить на эти вопросы.
Заданный вопрос имеет очень большую историю и
заведомо старше, чем исследования искусственных нейронных сетей.
Какие функции может вычислять человек? Если мы умеем
складывать и умножать числа, то мы можем точно вычислять многочлены и
рациональные функции (отношения многочленов) с рациональными коэффициентами от
рациональных же аргументов.
Можно, однако, задавать функции с помощью уравнений.
Если считать решения нескольких простых уравнений известными, то класс
вычисляемых функций расширится ‑ решения некоторых более общих уравнений
удастся выразить через эти, более простые функции.
Классический пример: если использовать радикалы ‑
решения уравнений xn=a, то можно явно получить
решения произвольных уравнений 2-й, 3-й и 4-й степеней. Так, функция 3-х
переменных a, b, c ‑ решение уравнения ax2 + bx + c=0 ‑ может быть точно
выражена с помощью сложения, умножения, деления и функции одного переменного ‑
квадратного корня.
Вопрос: можно ли представить решение любого
алгебраического уравнения с помощью радикалов, был окончательно и отрицательно
решен Абелем и Галуа ‑ уже уравнения 5-й степени неразрешимы в радикалах.
Все же можно подбирать другие простые функции
небольшого числа переменных ‑ сложнее, чем радикалы, но проще, чем общие
решения уравнений высоких степеней. Удастся ли с помощью этих функций построить
решение любого уравнения? Вопрос был настолько важен, что Гильберт в списке
своих проблем, которые, по его мнению, должны были определять развитие
математики XX века, под номером 13 поместил следующую задачу:
Представляется ли корень уравнения
x7 + ax3 + bx2 + cx + 1=0
(как функция коэффициентов) суперпозицией каких-либо непрерывных функций двух переменных?
Для уравнений 5-й и 6-й степени такое представление
возможно не только с помощью непрерывных, но даже аналитических функций.
Оказалось полезным абстрагироваться от уравнений и
поставить общий вопрос: можно ли произвольную непрерывную функцию n переменных получить с
помощью операций сложения, умножения и суперпозиции из непрерывных функций двух
переменных? Ответ оказался положительным! В серии работ [1-3] А.Н.Колмогоров,
затем В.И.Арнольд и вновь А.Н.Колмогоров решили эту проблему: можно получить
любую непрерывную функцию n
переменных с помощью операций сложения, умножения и суперпозиции из непрерывных
функций одного переменного.
Последняя теорема А.Н.Колмогорова [3] из этой серии
настолько проста и изящна, что мы чуть позже приведем ее целиком. А пока ‑
несколько замечаний о условиях теоремы.
От условия непрерывности можно отказаться ‑
тогда получится довольно тривиальный результат связанный, по существу, с
равномощностью отрезка и куба любой размерности. Условие непрерывности нельзя
значительно усилить: существуют аналитические функции многих переменных,
которые не допускают представления с помощью суперпозиции аналитических функций
двух переменных. Более того, все l
раз непрерывно дифференцируемые функции трех переменных нельзя представить в
виде суперпозиций функций двух переменных, каждая из которых дифференцируема [2l/3] раз и все частные
производные которых порядка [2l/3]
удовлетворяют условию Липшица (выражение [2l/3] означает целую часть числа 2l/3). Это доказано А.Г,Витушкиным [4].
А теперь ‑ теорема Колмогорова, завершившая серию исследований для непрерывных
функций:
Каждая непрерывная функция n переменных, заданная на единичном кубе n-мерного пространства,
представима в виде
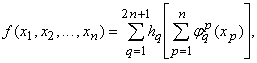 |
(1) |
где функции hq(u) непрерывны, а функции
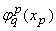 , кроме того, еще и стандартны, т.е. не зависят от выбора
функции f. , кроме того, еще и стандартны, т.е. не зависят от выбора
функции f.
В частности, каждая непрерывная функция двух переменных x, y представима в виде
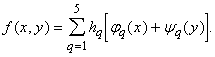 |
(2) |
Доказательство настолько просто, изящно и
поучительно, что мы приведем его практически полностью для случая n=2,
следуя изложению В.И.Арнольда [5]. Возможность представления (2) доказывается в
несколько этапов.
1. "Внутренние" функции jq(x)
и yq(y) представления (2)
совершенно не зависят от разлагаемой функции f(x, y).
Для определения этих функций нам понадобятся некоторые предварительные построения. Рассмотрим изображенный
на рис. 8 "город" –систему одинаковых "кварталов" (непересекающихся замкнутых квадратов), разделенных узкими "улицами"
одной и той же ширины. Уменьшим гомотетично наш "город" в
N раз; за центр гомотетии можно принять, например, точку A1
– мы получим новый" город", который будем называть "городом ранга 2". "Город ранга 3" точно также получается из "города ранга 2"
гомотетичным уменьшением с коэффициентом гомотетии
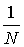 ;
"город ранга 4" получается гомотетичным уменьшением в N раз "города ранга 3" и т.д. Вообще "город ранга k"
получается из исходного "города" (который мы будем называть "городом первого ранга") гомотетичным уменьшением в
N k раз (с центром гомотетии в A1;
впрочем, выбор центра гомотетии не существенен для дальнейшего). ;
"город ранга 4" получается гомотетичным уменьшением в N раз "города ранга 3" и т.д. Вообще "город ранга k"
получается из исходного "города" (который мы будем называть "городом первого ранга") гомотетичным уменьшением в
N k раз (с центром гомотетии в A1;
впрочем, выбор центра гомотетии не существенен для дальнейшего).
 |
Построенную систему
"городов" мы назовем 1-й системой. "Город первого ранга
q-й системы" (q = 2,...,5) получается из изображенного на рис. 8 "города"
при помощи параллельного переноса, совмещающего точку A1 с точкой
Aq. Нетрудно понять, что "улицы" "города"
можно выбрать настолько узкими, что каждая точка плоскости будет покрыта по
крайней мере тремя кварталами наших пяти "городов первого ранга".
Точно так же "город k-го ранга" q-й системы (k = 2,3,...; q = 2,...,5)
получается из "города k-го ранга 1-й системы" параллельным переносом,
переводящим точку
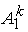 в точку в точку
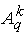 , где , где
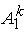 и и
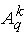 получаются из точек
A1 и Aq гомотетией, переводящей "город первого ранга" 1-й системы
(т.е. наш исходный "город") в "город k-го ранга" той же системы; при этом
каждая точка плоскости будет принадлежать кварталам по крайней мере
трех из пяти "городов" любого фиксированного ранга k. получаются из точек
A1 и Aq гомотетией, переводящей "город первого ранга" 1-й системы
(т.е. наш исходный "город") в "город k-го ранга" той же системы; при этом
каждая точка плоскости будет принадлежать кварталам по крайней мере
трех из пяти "городов" любого фиксированного ранга k.
Функцию
Fq(x, y) = jq(x) + yq(y)
(q = 1,2,...,5)
мы определим теперь так, чтобы она разделяла любые два "квартала" каждого "города" системы
q, т.е. чтобы множество значений, принимаемых
Fq(x, y) на определенном
"квартале" "города k-го ранга" (здесь k– произвольное фиксированное число)
q-й системы, не пересекалось с множеством значений, принимаемых
Fq(x, y) на любом другом
"квартале" того же "города". При этом нам, разумеется, будет достаточно рассматривать функцию
Fq(x, y) на единичном квадрате
(а не на всей плоскости).
Для того, чтобы функция
Fq(x, y) = jq(x) + yq(y) разделяла
"кварталы" "города первого ранга", можно потребовать, например, чтобы
jq(x) на проекциях
"кварталов" "города" на ось x весьма мало отличалась от различных целых чисел, а
yq(y) на проекциях
“кварталов” на ось y весьма мало отличалась от различных кратных
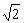 (ибо (ибо
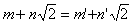 при целых
m, n, m', n', лишь если m = m', n = n'). При этом наложенные условия не определяют пока еще,
разумеется, функций
jq(x) и
yq(y) (на "улицах" функция
Fq(x, y) = jq(x) + yq(y) вообще пока может
задаваться совершенно произвольно); используя это, можно подобрать границы
значений
jq(x) и
yq(y) на "кварталах"
"города второго ранга" так, чтобы функция
Fq(x, y) = jq(x) + yq(y) разделяла не только
"кварталы" "города 1-го ранга", но и “кварталы”
"города 2-го ранга". Намеченную программу можно осуществить, если N достаточно велико
(так что кварталы последующих рангов не соединяют кварталы предыдущих). А.Н. Колмогоров выбрал
N = 18. Привлекая подобным же образом к рассмотрению
"города" последующих рангов и уточняя каждый раз значения функций
jq(x) и
yq(y), мы в пределе получим непрерывные функции
jq(x) и
yq(y)(можно даже
потребовать, чтобы они были монотонными), удовлетворяющие поставленным
условиям. при целых
m, n, m', n', лишь если m = m', n = n'). При этом наложенные условия не определяют пока еще,
разумеется, функций
jq(x) и
yq(y) (на "улицах" функция
Fq(x, y) = jq(x) + yq(y) вообще пока может
задаваться совершенно произвольно); используя это, можно подобрать границы
значений
jq(x) и
yq(y) на "кварталах"
"города второго ранга" так, чтобы функция
Fq(x, y) = jq(x) + yq(y) разделяла не только
"кварталы" "города 1-го ранга", но и “кварталы”
"города 2-го ранга". Намеченную программу можно осуществить, если N достаточно велико
(так что кварталы последующих рангов не соединяют кварталы предыдущих). А.Н. Колмогоров выбрал
N = 18. Привлекая подобным же образом к рассмотрению
"города" последующих рангов и уточняя каждый раз значения функций
jq(x) и
yq(y), мы в пределе получим непрерывные функции
jq(x) и
yq(y)(можно даже
потребовать, чтобы они были монотонными), удовлетворяющие поставленным
условиям.
2. Функции hq(u) разложения (2),
напротив того, существенно зависят от исходной функции
f(x, y).
Для построения этих функций докажем прежде всего, что любую
непрерывную функцию f(x, y)
двух переменных x и y, заданную на единичном квадрате, можно представить в виде
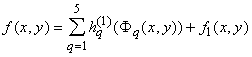 , , |
(3) |
где Fq(x, y) = jq(x) + yq(y) – функции,
построенные выше, и
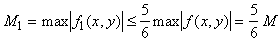 , , |
(3а) |
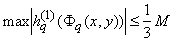 ,
(q = 1,...,5). ,
(q = 1,...,5). |
(3б) |
Выберем ранг
k столь большим, чтобы колебание (т.е. разность наибольшего и наименьшего значений) функции
f(x, y) на каждом "квартале" любого из "городов ранга
k" не превосходило
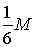 ; это, разумеется, возможно, так как с ростом ранга
k размеры "кварталов" уменьшаются неограниченно. Далее, пусть ; это, разумеется, возможно, так как с ростом ранга
k размеры "кварталов" уменьшаются неограниченно. Далее, пусть
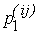 – определенный "квартал" "города 1-й системы"
(и выбранного ранга k); в таком случае (непрерывная) функция
F1(x, y) принимает на этом "квартале" значения, принадлежащие определенному сегменту – определенный "квартал" "города 1-й системы"
(и выбранного ранга k); в таком случае (непрерывная) функция
F1(x, y) принимает на этом "квартале" значения, принадлежащие определенному сегменту
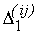 числовой оси (причем в силу определения функции
F1 этот сегмент не пересекается с сегментами значений, принимаемых
F1 на всех других "кварталах"). Положим теперь функцию числовой оси (причем в силу определения функции
F1 этот сегмент не пересекается с сегментами значений, принимаемых
F1 на всех других "кварталах"). Положим теперь функцию
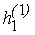 на сегменте на сегменте
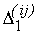 постоянной, равной постоянной, равной
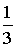 значения, принимаемого функцией
f(x, y) в какой-либо (безразлично какой) внутренней точке значения, принимаемого функцией
f(x, y) в какой-либо (безразлично какой) внутренней точке
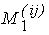 квартала квартала
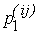 (эту точку можно назвать "центром квартала"). Таким же образом мы определим функцию (эту точку можно назвать "центром квартала"). Таким же образом мы определим функцию
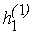 на любом другом из сегментов, задаваемых значениями функции
F1(x, y) на "кварталах" "города
k-го ранга" 1-й системы; при этом все значения на любом другом из сегментов, задаваемых значениями функции
F1(x, y) на "кварталах" "города
k-го ранга" 1-й системы; при этом все значения
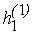 будут по модулю не превосходить будут по модулю не превосходить
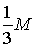 (ибо значение
f(x, y) в "центре" любого "квартала" по модулю не превосходит M). Доопределим теперь функцию (ибо значение
f(x, y) в "центре" любого "квартала" по модулю не превосходит M). Доопределим теперь функцию
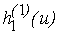 при тех значениях аргумента
u, при каких она еще не определена, произвольно, с тем лишь,
чтобы она была непрерывна и чтобы выполнялось неравенство (3б); совершенно аналогично определим и все остальные функции при тех значениях аргумента
u, при каких она еще не определена, произвольно, с тем лишь,
чтобы она была непрерывна и чтобы выполнялось неравенство (3б); совершенно аналогично определим и все остальные функции
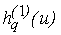 (q = 2,...,5). (q = 2,...,5).
Докажем теперь, что разность
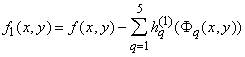
удовлетворяет условию (3а), т.е. что
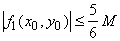 , ,
где (x0, y0)– произвольная точка единичного квадрата. Эта точка
(как и все точки плоскости) принадлежит по крайней мере трем кварталам "городов ранга k";
поэтому заведомо найдутся такие три из пяти функций
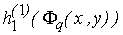 , которые принимают в точке
(x0, y0) значение, равное , которые принимают в точке
(x0, y0) значение, равное
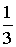 значения
f(x, y) в "центре" соответствующего "квартала", т.е. отличающееся от значения
f(x, y) в "центре" соответствующего "квартала", т.е. отличающееся от
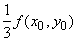 не более чем на не более чем на
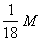 (ибо колебание
f(x, y) на каждом квартале не превосходит (ибо колебание
f(x, y) на каждом квартале не превосходит
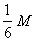 ); сумма этих трех значений ); сумма этих трех значений
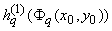 будет отличаться от
f(x0, y0) по модулю не более чем на будет отличаться от
f(x0, y0) по модулю не более чем на
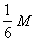 . А так как каждое из оставшихся двух чисел . А так как каждое из оставшихся двух чисел
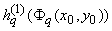 в силу (3) по модулю не превосходит в силу (3) по модулю не превосходит
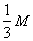 то мы получаем: то мы получаем:
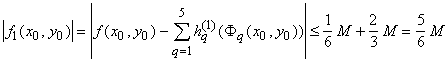 , ,
что и доказывает (3а).
Применим теперь то же разложение (3) к входящей в (3) функции
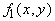 ; мы получим: ; мы получим:
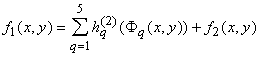
или
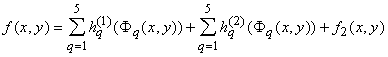 , ,
где
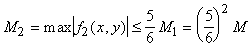
и 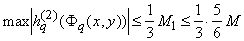 ( (
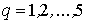 ). ).
Затем мы применим разложение (3) к полученной функции
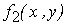 и т.д.; после
n-кратного применения этого разложения мы будем иметь: и т.д.; после
n-кратного применения этого разложения мы будем иметь:
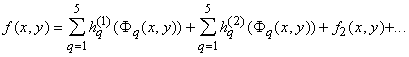
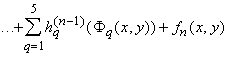 , ,
где
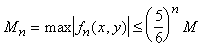
и
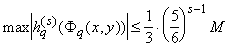 ( (
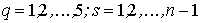 ). ).
Последние оценки показывают, что при
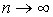 получим: получим:
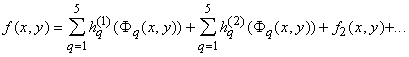
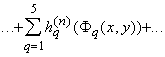
где стоящий справа бесконечный ряд сходится равномерно; также и каждый из пяти
рядов
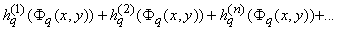 (
(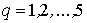 ) )
сходится равномерно, что позволяет ввести обозначения
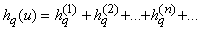 ( (
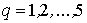 ). ).
Итак, окончательно получаем:
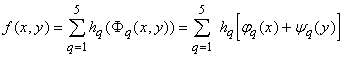 , ,
то есть требуемое разложение (2).
До сих пор речь шла о точном представлении функций многих переменных с помощью функций
одного переменного. Оказалось, что в классе непрерывных функций такое
представление возможно. Но кроме вопроса о точном представлении существует еще
один ‑ об аппроксимации. Можно
даже предположить, что он важнее ‑ вычисление большинства функций
производится приближенно даже при наличии «точных» формул.
Приближение функций многочленами и рациональными
функциями имеет историю, еще более давнюю, чем проблема точного представления.
Знаменитая теорема Вейерштрасса утверждает,
что непрерывную функцию нескольких переменных 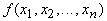 на замкнутом ограниченном множестве Q можно равномерно приблизить
последовательностью полиномов: для любого e>0 существует такой
многочлен
на замкнутом ограниченном множестве Q можно равномерно приблизить
последовательностью полиномов: для любого e>0 существует такой
многочлен 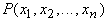 , что , что
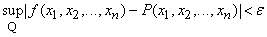 . .
Чтобы сформулировать обобщения и усиления теоремы
Вейерштрасса, необходимо перейти к несколько более абстрактному языку.
Рассмотрим компактное пространство X
и алгебру C(X) непрерывных функций на
X с вещественными значениями.
Сильным обобщением теоремы о возможности
равномерного приближения непрерывных функций многочленами является теорема Стоуна [6,7]:
Пусть E Í C(X) ‑ замкнутая подалгебра в C(X),
1Î E и функции из E разделяют точки в X (то есть для
любых различных x,y Î
X существует такая функция g Î
E, что g(x) ¹ g(y)). Тогда E=C(X).
Теорема Стоуна обобщает теорему Вейерштрасса по двум
направлениям. Во-первых, рассматриваются функции на произвольном компакте, а не
только функции многих действительных переменных. Во-вторых, доказано
утверждение, новое даже для функций одного переменного (не говоря уже о
многих): плотно не только множество многочленов от координатных функций, но
вообще кольцо многочленов от любого набора функций, разделяющих точки.
Следовательно, плотно множество тригонометрических многочленов, множество
линейных комбинаций функций вида exp[-(x-x0, Q(x-x0))],
где (x,Qx) ‑ положительно определенная квадратичная форма и др.
Дан рецепт конструирования таких обобщений:
достаточно взять произвольный набор функций, разделяющих точки, построить
кольцо многочленов от них ‑ и получим плотное в C(X) множество функций.
Разложения по ортогональным системам функций (ряды Фурье и их многочисленные обобщения) не дают,
вообще говоря, равномерного приближения разлагаемых функций ‑ как
правило, можно гарантировать лишь монотонное стремление к нулю интеграла
квадрата остатка «функция минус приближение» с какой-либо положительной весовой
функцией. Все же, обращаясь к задаче аппроксимации, нельзя забывать об
ортогональных разложениях. Для ряда прикладных задач простота получения
коэффициентов такого разложения может оказаться важнее, чем отсутствие
гарантированной равномерности приближения.
Так существуют ли функции многих переменных? В
каком-то смысле ‑ да, в каком-то ‑ нет. Все непрерывные функции
многих переменных могут быть получены из непрерывных функций одного переменного
с помощью линейных операций и суперпозиции. Требования гладкости и
аналитичности существенно усложняют вопрос. На этом фоне совершенно неожиданно
выглядит тот факт, что любой многочлен от
многих переменных может быть получен из одного произвольного нелинейного
многочлена от одного переменного с помощью линейных операций и суперпозиции.
Простое доказательство этой теоремы будет дано в разделе 6.
5. Универсальные аппроксимационные способности произвольной
нелинейности и обобщенная теорема Стоуна
В этом разделе для множеств непрерывных функций,
замкнутых относительно любой нелинейной операции (а не только для колец),
доказана обобщенная аппроксимационная теорема Стоуна. Это интерпретируется как
утверждение о универсальных аппроксимационных возможностях произвольной
нелинейности: с помощью линейных операций и каскадного соединения можно из
произвольного нелинейного элемента получить устройство, вычисляющее любую
непрерывную функцию с любой наперед заданной точностью.
Рассмотрим компактное пространство X и алгебру C(X) непрерывных функций на X
с вещественными значениями.
Кроме аппроксимации функций многочленами и их
обобщениями из колец функций, разделяющих точки, в последнее время все большее
внимание уделяется приближению функций многих переменных с помощью линейных
операций и суперпозиций функций одного переменного. Такое приближение
осуществляется специальными формальными "устройствами" – нейронными
сетями. Каждая сеть состоит из формальных нейронов. Нейрон получает на входе вектор
сигналов x, вычисляет его скалярное произведение на вектор весов
a и некоторую функцию одного переменного
j (x,
a). Результат рассылается на
входы других нейронов или передается на выход. Таким образом, нейронные сети
вычисляют суперпозиции простых функций одного переменного и их линейных
комбинаций.
Доказан ряд теорем [8-10] об аппроксимации
непрерывных функций многих переменных нейронными сетями с использованием
практически произвольной непрерывной функции одного переменного. В данном
разделе мы покажем, что эта функция действительно может быть произвольной и
докажем обобщенную теорему Стоуна, естественным образом охватывающую и
классическую теорему Стоуна, и аппроксимацию функций многих переменных
суперпозициями и линейными комбинациями функций одного переменного.
Чтобы получить требуемое обобщение, перейдем от
рассмотрения колец функций к изучению их алгебр, замкнутых относительно
некоторой нелинейной унарной операции.
Пусть EÍ C (X) ‑
линейное пространство, C(R) ‑ пространство непрерывных функций на действительной
оси R, fÎ С(R) ‑
нелинейная функция и для любого gÎ E
выполнено f(g)ÎE.
В этом случае будем говорить, что E замкнуто относительно нелинейной унарной операции f.
Очевидный пример: множество функций n переменных, которые можно точно
представить, используя заданную функцию одного переменного и линейные функции,
является линейным пространством, замкнутым относительно нелинейной унарной
операции f.
Замечание. Линейное пространство EÍC(X) замкнуто относительно нелинейной
операции f(x)=x2 тогда и только тогда, когда E является кольцом.
Действительно, 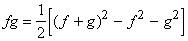 поэтому для линейного
пространства EÍC(X) замкнутость
относительно унарной операции f(x)=x2 равносильна замкнутости
относительно произведения функций. поэтому для линейного
пространства EÍC(X) замкнутость
относительно унарной операции f(x)=x2 равносильна замкнутости
относительно произведения функций.
Согласно приведенному замечанию, теорема Стоуна может быть переформулирована так.
Пусть EÍC(X) ‑ замкнутое линейное
подпространство в C(X), 1ÎE,
функции из E разделяют точки в X и E
замкнуто относительно нелинейной унарной операции f(x)=x2. Тогда E=C(X).
Наше обобщение теоремы Стоуна состоит в замене f(x)=x2 на произвольную нелинейную
непрерывную функцию.
Теорема 1. Пусть EÍC(X) ‑
замкнутое линейное подпространство в C(X), 1ÎE,
функции из E разделяют точки в X и E
замкнуто относительно нелинейной унарной операции fÎC(R).
Тогда E=C(X).
Доказательство. Рассмотрим множество всех таких pÎC(R),
что p(E)ÍE,
то есть для любого gÎE выполнено:
p(g)ÎE. Обозначим это множество
PE. Оно обладает следующими свойствами:
- PE ‑ полугруппа относительно суперпозиции функций;
- PE ‑ замкнутое линейное подпространство в C(R)
(в топологии равномерной сходимости на компактах);
- 1ÎPE и id
ÎPE (id(x)
ºx).
- PE включает хоть одну непрерывную нелинейную функцию.
Дальнейшее следует из теоремы 2, которая является, по существу, подготовительной теоремой о полугруппах функций.
Теорема 2. Пусть множество PÍC(R)
удовлетворяет условиям 1-4. Тогда P=C(R).
Доказательство опирается на три леммы.
Лемма 1. В условиях теоремы 2 существует дважды
непрерывно дифференцируемая функция gÎP,
не являющаяся линейной.
Доказательство. Пусть v(x)ÎC¥(R),
v(x)=0 при |x| >1, òRv(x)dx=1. Рассмотрим
оператор осреднения
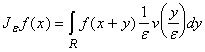
Для любого e>0 выполнено: 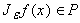 . .
Действительно, f(x+y)ÎE для каждого фиксированного
y (т.к. константы принадлежат E и E замкнуто относительно линейных операций и суперпозиции функций). Интеграл
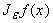 . принадлежит E, так как E является замкнутым линейным
подпространством в C(R), а этот интеграл ‑ пределом конечных сумм. . принадлежит E, так как E является замкнутым линейным
подпространством в C(R), а этот интеграл ‑ пределом конечных сумм.
Функция 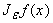 принадлежит C¥(R) так как
принадлежит C¥(R) так как
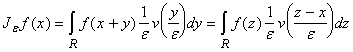
(напомним, что v – функция с компактным носителем).
Существует такое e>0, что функция g=
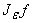 не является линейной,
поскольку не является линейной,
поскольку 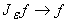 при
e
®0, пространство линейных
функций замкнуто, а f не является линейной функцией. Таким образом, в
предположениях леммы существует нелинейная функция gÎPÇC¥(R),
которую можно выбрать в виде g= при
e
®0, пространство линейных
функций замкнуто, а f не является линейной функцией. Таким образом, в
предположениях леммы существует нелинейная функция gÎPÇC¥(R),
которую можно выбрать в виде g=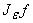
Лемма 2. Пусть в условиях теоремы 2 существует дважды непрерывно дифференцируемая функция
gÎP, не являющаяся линейной.
Тогда функция q(x)=x2 принадлежит P.
Доказательство. Существует точка x0, для которой
g¢¢(x0)
¹0.
Обозначим r(x)=2(g(x+x0)‑g(x0)‑xg¢(x0))/g¢¢(x0).
Очевидно, что rÎP,
r(0)=0, r¢(0)=0,
r¢¢(0)=2,
r(x)=x2+o(x2). Поэтому
r(ex)/e2 ® x2
при e ® 0.
Поскольку P замкнуто, получаем: функция q(x)=x2 принадлежит P.
Лемма 3. Пусть в условиях теоремы 2 функция q(x)=x2 принадлежит P.
Тогда P является кольцом – для любых f,gÎP
их произведение fgÎP.
Доказательство. Действительно, 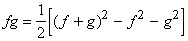 и,
так как P замкнуто относительно суперпозиции и линейных операций, то
fgÎP. и,
так как P замкнуто относительно суперпозиции и линейных операций, то
fgÎP.
Доказательство теоремы 2 заканчивается обращением к
классической теореме Вейерштрасса о приближении функций многочленами: из лемм
1-3 следует, что в условиях теоремы 2 P является кольцом и, в частности, содержит все многочлены (которые
получаются из 1 и id с помощью умножения и линейных операций). По
теореме Вейерштрасса отсюда следует, что P=C(R).
Теоремы 1,2 можно трактовать как утверждения о
универсальных аппроксимационных свойствах любой нелинейности: с помощью
линейных операций и каскадного соединения можно из произвольных нелинейных
элементов получить любой требуемый результат с любой наперед заданной
точностью.
6. Точное представление многочленов от многих переменных с помощью одного произвольного
многочлена от одного переменного, линейных операций и суперпозиции
В этом разделе исследуются полугруппы полиномов от
одного переменного относительно суперпозиции. Показано, что если такая
полугруппа содержит все многочлены первой степени и хотя бы один – более
высокой, то она включает все многочлены. На основании этого факта доказано, что
всегда возможно представить многочлен от многих переменных суперпозициями
произвольного нелинейного многочлена от одного переменного и линейных функций.
Вернемся к классическому вопросу о представлении
функций многих переменных с помощью функций меньшего числа переменных. Следует
еще раз заметить, что классических вопроса существует не один, а два:
- Можно ли получить точное представление функции многих переменных с помощью
суперпозиции функций меньшего числа переменных?
- Можно ли получить сколь угодно точную аппроксимацию функции многих переменных с
помощью некоторых более простых функций и операций?
В рамках первого вопроса особый интерес представляют
конструкции, в которых для точного представления всех функций многих переменных
используется один и тот же набор функций одного переменного.
Традиционно считается, что эти функции должны иметь
весьма специальный и довольно экзотический вид, например, как в обсуждавшейся
выше теореме Колмогорова, где использовались существенно негладкие функции.
Напротив, свобода в выборе функций одного
переменного для решения второго вопроса при том же самоограничении ( один набор
функций одного переменного ‑ для приближенного представления всех функций
многих переменных) очень велика. Для этого, как показано в предыдущем разделе,
можно использовать практически любую нелинейную функцию и достаточно всего
одной.
Далее доказываются теоремы, относящиеся к первому
вопросу (точное представление). В частности, показано, что можно точно
представить любой многочлен от многих переменных с помощью суперпозиций
произвольного нелинейного многочлена от одного переменного и линейных функций.
Следовательно особенной пропасти между 1-м и 2-м вопросом не существует. Именно
это обстоятельство побудило нас включить в книгу данный раздел.
Пусть R[X] ‑ кольцо многочленов от одного
переменного над полем R, EÌR[X]
‑ линейное пространство многочленов над R.
Предложение 1. Если E замкнуто относительно суперпозиции многочленов, содержит все
многочлены первой степени и хотя бы один многочлен p(x) степени m>1, то E=R[X].
Доказательство. Заметим, что степень многочлена p¢(x)=p(x+1)‑p(x)
равна m‑1, и p¢(x)ÎE,
так как E содержит многочлены первой
степени (поэтому x+1ÎE), замкнуто относительно
суперпозиции (поэтому p(x+1)ÎE)
и линейных операций (поэтому p¢(x)ÎE).
Если m>2,
то понижаем степень с помощью конечных разностей (переходим к p¢,
p¢¢ и т.д.), пока не получим
многочлен второй степени. Вычитая из него линейную часть и умножая на
константу, получаем: x2ÎE.
Поэтому для любого fÎE
имеем f 2ÎE
(т.к. E ‑ полугруппа). Дальнейшее очевидно: как неоднократно
отмечалось выше, отсюда следует, что для любых f,gÎE
их произведение fgÎE а с помощью умножения и
сложения многочленов первой степени порождается все кольцо R[X].
Перейдем к задаче представления многочленов от
многих переменных. Обозначим R[X1, ..., Xn]
кольцо многочленов от n переменных над полем R.
Для каждого многочлена от одного переменного введем
множество тех многочленов, которые можно выразить с его помощью, используя
суперпозиции и линейные функции. Пусть p
– многочлен от одного переменного, Ep[X1, ..., Xn]
– множество многочленов от n
переменных, которое можно получить из p
и многочленов первой степени, принадлежащих R[X1, ..., Xn],
с помощью операций суперпозиции, сложения и умножения на число.
Следующие два предложения дают удобную для дальнейшего характеризацию
Ep[X1, ..., Xn] и следуют непосредственно
из определений.
Предложение 2. Множество Ep[X1, ..., Xn] является линейным
пространством над R и для любого
многочлена g(x1, ... ,xn)
из Ep[X1, ..., Xn]
p(g(x1, ... ,xn))ÎEp[X1,
..., Xn].
Предложение 3.Для данного p семейство линейных подпространств
LÍR[X1, ..., Xn],
содержащих все многочлены первой степени и удовлетворяющих условию
если
g(x1, ... ,xn)ÎL,
то p(g(x1, ... ,xn))ÎL,
замкнуто относительно пересечений. Минимальным по включению элементом этого семейства является
Ep[X1, ..., Xn].
Для любого линейного подпространства EÍR[X1,
..., Xn] рассмотрим множество алгебраических унарных операций, которые переводят элементы E
в элементы E:
PE={pÎR[X]
| p(g(x1, ... ,xn))ÎE
для любого g(x1, ... ,xn)ÎE}.
Предложение 4. Для любого линейного подпространства EÍR[X1, ... ,Xn]
множество полиномов PE является линейным пространством над R, замкнуто относительно суперпозиции и
содержит все однородные многочлены первой степени.
Если линейное пространство E содержит 1, а PE включает хотя бы один
многочлен, степени m>1 (т.е.
нелинейный), то PE=R[X].
Доказательство. Замкнутость PE
относительно суперпозиции следует из определения, все однородные полиномы
первой степени входят в PE, поскольку E является линейным пространством,
отсюда также следует, что PE является линейным
пространством. Наконец, если 1ÎE и
PE содержит многочлен степени m>1, то 1ÎPE,
тогда PE=R[X] по предложению 1.
Теорема 3. Пусть EÍR[X1, ..., Xn] – линейное
подпространство, PE содержит хотя бы один
многочлен степени m>1 и 1ÎE, тогда E является кольцом
(с единицей).
Доказательство. По предложению 4 в условиях теоремы PE=R[X]. В частности, x2ÎPE. Это означает, что для
любого fÎE также и f2ÎE.
Поэтому для любых f,gÎE получаем: fgÎE.
Теорема 4. Для любого многочлена p степени m>1
Ep[X1, ..., Xn]=R[X1,
..., Xn]
Доказательство. Заметим, что E=Ep[X1, ..., Xn]
– линейное подпространство в R[X1, ..., Xn], PE
содержит хотя бы один многочлен (p)
степени m>1 и E содержит все многочлены первой степени (и поэтому также 1). В
силу теоремы 3, E является кольцом, а
так как оно содержит все многочлены первой степени, то совпадает с R[X1, ..., Xn],
поскольку, используя умножение и сложение можно из этих многочленов получить
любой.
Таким образом, из p и многочленов первой степени с помощью операций суперпозиции,
сложения и умножения на число можно получить все элементы R[X1, ..., Xn].
7. Нейронные сети – универсальные аппроксимирующие устройства и могут с
любой точностью имитировать любой непрерывный автомат
Класс функций, вычислимый с помощью нейронных сетей,
замкнут относительно линейных операций. Действительно, пусть есть нейронные
сети S1, S2, ..., Sk, которые вычисляют функции F1, F2, ..., Fk от вектора входных сигналов
x. Линейная комбинация
a 0 +
a 1 F1 +
a 2 F2 + ... +
a k Fk
вычисляется сумматором (рис. 2) с весами
a 0,
a 1,
a 2, ...,
a k,
на вход которого подаются выходные сигналы сетей S1, S2, ..., Sk.
Разница в числе тактов функционирования этих сетей до получения ответа легко компенсируется «линиями
задержки», составленными из связей (рис. 6) с единичным весом.
Кроме того, класс функций, вычислимый с помощью
нейронных сетей, замкнут относительно унарной операции, осуществляемой
нелинейным преобразователем сигнала, входящим в состав нейрона (см. рис. 3, 5):
если сеть S вычисляет функцию F, то, подавая выход этой
сети на вход нелинейного преобразователя (рис. 3), получим на его выходе
функцию j(F).
Тем самым, по теореме 1 множество функций,
вычислимых нейронными сетями с заданной непрерывной нелинейной
характеристической функцией, плотно в пространстве непрерывных функций от
входных сигналов.
Теперь ‑ об имитации гладких автоматов с
помощью нейронных сетей. Если есть возможность с любой точностью приблизить
любую непрерывную функцию и нет ограничений на способы соединения устройств, то
можно сколь угодно точно имитировать работу любого непрерывного автомата.
Покажем это.
Каждый автомат имеет несколько входов (n), несколько выходов (p) и конечный набор (s)
параметров состояния. Он вычисляет s+p
функций от n+s переменных. Аргументы этих функций ‑ входные сигналы (их n) и
текущие параметры состояния (их s). Значения функций – выходные сигналы
(их p) и параметры состояния на
следующем шаге (их s). Каждый такой
автомат можно представить как систему из s+p более простых автоматов (рис. 9). Эти
простые автоматы вычисляют по одной функции от n+s переменных. Смена
состояний достигается за счет того, что часть значений этих функций на
следующем шаге становится аргументами – так соединены автоматы (см. рис. 9).
Таким образом, без потери общности можно
рассматривать сеть автоматов как набор устройств, каждое из которых вычисляет
функцию нескольких переменных f(x1, ... ,xn). Этот простой, но
фундаментальный факт позволяет использовать предыдущие результаты. Нейронные
сети позволяют с любой точностью вычислять произвольную непрерывную функцию f(x1,
... ,xn).
Следовательно, с их помощью можно сколь угодно точно аппроксимировать
функционирование любого непрерывного автомата.
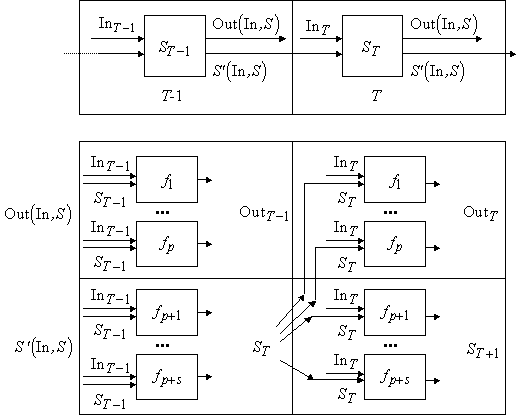 |
| Рис. 9. Представление
общего автомата с помощью модулей, вычисляющих функции многих переменных от
входных сигналов: на верхней схеме представлено функционирование автомата, на
нижней он разложен на отдельные модули. |
Приняты обозначения:
In ‑ входные сигналы, Out ‑ выходные сигналы, S ‑ параметры состояния,
T ‑ дискретное время, Out(In,S) ‑ зависимость выходных сигналов от значений
входных и параметров состояния, S¢(In,S) ‑
зависимость состояния в следующий момент дискретного времени от входных сигналов и текущего состояния,
f1-fp ‑ функции переменных (In,S) ‑ компоненты вектора
Out(In,S), fp+1-fp+s ‑ функции переменных (In,S) ‑
компоненты вектора S¢(In,S),
индексами T, T±1 обозначены соответствующие
моменты времени.
Главный вопрос этой главы: что могут нейронные сети.
Ответ получен: нейронные сети могут все. Остается открытым другой вопрос ‑
как их этому научить?
Работа над главой была поддержана Красноярским краевым фондом науки, грант 6F0124.
Литература
- Колмогоров А.Н. О представлении непрерывных
функций нескольких переменных суперпозициями непрерывных функций меньшего числа
переменных. Докл. АН СССР, 1956. Т. 108, No. 2. С.179-182.
- Арнольд В.И. О функциях трех переменных. Докл. АН
СССР, 1957. Т. 114, No. 4. С. 679-681.
- Колмогоров А.Н. О представлении непрерывных
функций нескольких переменных в виде суперпозиции непрерывных функций одного
переменного. Докл. АН СССР, 1957. Т. 114, No. 5. С.
953-956.
- Витушкин А.Г. О многомерных вариациях. М.: Физматгиз, 1955.
- Арнольд В.И. О представлении функций нескольких переменных в виде суперпозиции функций
меньшего числа переменных // Математическое просвещение, 19 № с. 41-61.
- Stone M.N. The generalized Weierstrass approximation theorem. Math. Mag., 1948. V.21. PP.
167-183, 237-254.
- Шефер Х. Топологические векторные пространства. М.: Мир, 1971. 360 с.
- Cybenko G. Approximation by superposition of a sigmoidal function. Mathematics of Control,
Signals, and Systems, 1989. Vol. 2. PP. 303 - 314.
- Hornik K., Stinchcombe M., White H. Multilayer feedforward networks are universal
approximators. Neural Networks. 1989. Vol. 2. PP. 359 - 366.
- Kochenov D.A., Rossiev D.A. Approximations of functions of C[A,B] class by neural-net
predictors (architectures and results). AMSE Transaction, Scientific Siberian,
A. 1993, Vol. 6. Neurocomputing. PP. 189-203. Tassin, France.
- Gilev S.E., Gorban A.N. On completness of the class of functions computable by neural
networks. Proc. of the World Congress on Neural Networks (WCNN'96). Sept.
15-18, 1996, San Diego, CA, Lawrens Erlbaum Accociates, 1996. PP. 984-991.
- Горбань А.Н., Россиев Д.А. Нейронные сети на
персональном компьютере. Новосибирск: Наука (Сиб. отделение), 1996. 276 с.
1 660036, Красноярск-36, ВЦК СО РАН. E-mail:
|
 материалы
материалы  справочник
справочник  форум
форум  гостевая
гостевая  ссылки
ссылки